Parametric Equation Anyone?

Calculus Level 2

A parametric equation is a way of representing a relationship between two variables (say, $x$ and $y$ ) by introducing a third variable, say $t$ , and setting up a set of equations as a function of this third variable.

Suppose we have the following equation of an ellipse:

$x^2 + 4y^2 = R^2.$

Which set of parametric equations will trace out a similar ellipse?

A. $x(t) = R\cos(t), y(t) = \frac{R\sin(t)}{2}$

B. $x(t) = R\sin(t), y(t) = \frac{R\cos(t)}{2}$

C. $x(t) = R\cos(t), y(t) = 2R\sin(t)$

D. $x(t) = 2R\cos(t), y(t) = R\sin(t)$

A B C D Two of these Three of these All of these None of these

2 solutions

Geoff Pilling
Dec 31, 2016

If you trace out A and B , for $t: 0 \rightarrow 2\pi$ then you get the ellipse:

$x^2 + 4y^2 = R^2$

If you trace out C , for $t: 0 \rightarrow 2\pi$ then you get the ellipse:

$x^2 + \frac{y^2}{4} = R^2$

If you trace out D , for $t: 0 \rightarrow 2\pi$ then you get the ellipse:

$\frac{x^2}{4} + y^2 = R^2$

Therefore, A and B both trace out the ellipse we want, so that's $\boxed{\text{two of these}}$ .

Why not B? Also, is the curve supposed to be similar (proportional) or actually identical? I said "three of these" because A,B, and D gave curves with the semi-major axis (x) twice as long as the semi-minor axis (y).

Steven Chase - 4 years, 5 months ago

Yes. A and B are the correct answers. I had a typo in my original solution that I've fixed.

Geoff Pilling - 4 years, 5 months ago

@Steven Chase, B is also included as an answer - see the last line of the Solution explanation.

I think the question actually asks for the curve that is identical to the provided equation of an ellipse as if otherwise, you could even say C is also an answer - it is just D rotated by 90 degrees!

Jel A - 2 years, 4 months ago

Lara Vrabac
Apr 7, 2020

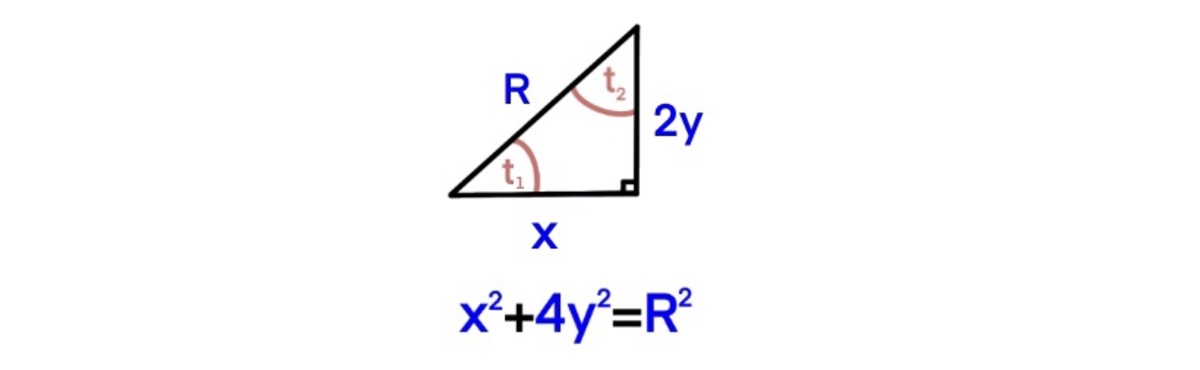
Imagine a right triangle with side lengths $x, 2y$ and $R$ , and acute angles $t_1$ and $t_2$ .

We can then see that:

$x=R\cos(t_1)$ $\\y=\dfrac{R}{2}\sin(t_1)$

And from the other angle:

$x=R\sin(t_2)$ $\\y=\dfrac{R}{2}\cos(t_2)$

Which are ellipses congruent to the one given, so the correct answers are A and B.

Parametric Equation Anyone?

2 solutions

0 pending reports