Paranormal
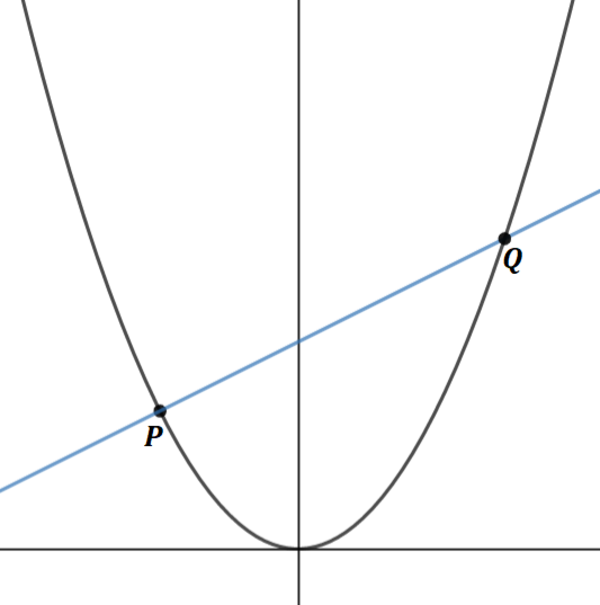
If P Q is a normal of the parabola y = k 1 x 2 at P , and the lowest possible y -coordinate of Q is 2 0 , find k .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
This isn't really an elegant solution. Also I'm a bit of a LaTex noob so please forgive the formatting.
y = k x 2
We shall first find the equation of the normal line at x = p .
The gradient of the normal line is − d y / d x 1 ∣ = − 2 x / k 1 ∣ x = p = 2 p − k .
We let y t a n be the normal line.
y t a n ( x ) = 2 p − k x + c
y t a n ( p ) = k p 2
⇒ 2 p − k p + c = k p 2
⇒ c = k p 2 + 2 k
⇒ y t a n = 2 k k 2 − 2 p 2 − 2 p k x
y t a n ( x ) and y = k x 2 intersect at points P ( p , k p 2 ) and Q ( q , k q 2 ) so we solve 2 k k 2 − 2 p 2 − 2 p k q = k q 2 for q .
Thus q = 2 p − ( k 2 + 2 p 2 ) (or q = p which is not desired in this case)
We want the minimum of k q 2 to be 20. So we define the function f = k q 2 = 4 k p 2 ( k 2 + 2 p 2 ) 2
Next, we solve d p d f = 0 for p in terms of k and substitute it back in to f .
d p d f = 2 p 3 k ( 2 p 2 + k 2 ) ( 2 p 2 − k 2 )
2 p 3 k ( 2 p 2 + k 2 ) ( 2 p 2 − k 2 ) = 0
⇒ 2 p 2 + k 2 = 0 or 2 p 2 − k 2 = 0
⇒ p 2 = 2 − k 2 or p 2 = 2 k 2
f ∣ p 2 = 2 − k 2 = 4 k ( 2 − k 2 ) ( k 2 + 2 ( 2 − k 2 ) ) 2
= 4 k ( 2 − k 2 ) 0 2
= 0
(this answer doesn't mean much since p is supposed to be a real number anyways)
f ∣ p 2 = 2 k 2 = 4 k ( 2 k 2 ) ( k 2 + 2 ( 2 k 2 ) ) 2 = 2 k .
If we equate 2 k = 2 0 , we obtain the desired k = 1 0 . And for completeness, 1 0 q 2 = 2 0 when p = ± 5 2 . 1 0 q 2 > 2 0 for any other values of p .
Let P be any point on the parabola y = k x 2 ⟹ P = ( a , k a 2 ) for some real a .
The slope of the normal at point P is given by − d x d y ] x = a 1 = − k 2 x ] x = a 1 = − 2 a k Using the Point-Slope form, the equation of line P Q is, y − k a 2 = − 2 a k ( x − a ) ⟹ 2 a k x + y − k a 2 − 2 k = 0 In order to find the intersection points ( P and Q ) of line P Q and parabola y = k x 2 , we need to solve the pair of equations, ⎩ ⎪ ⎨ ⎪ ⎧ 2 a k x + y − k a 2 − 2 k = 0 y = k x 2 This leads us to the solutions P Q = ( a , k a 2 ) = ( − 2 a k 2 − a , 4 a 2 k 3 + k a 2 + k ) So, we are given that min ( 4 a 2 k 3 + k a 2 + k ) = 2 0 . Differentiating with respect to a and equating to 0 , d a d ( 4 a 2 k 3 + k a 2 + k ) = 0 ⟹ − 2 a 3 k 3 + k 2 a ⟹ k = 2 a = 0 Therefore , a = 2 k is a critical point, and is in fact, the point of minima. So, when a = 2 k 2 , the expression 4 a 2 k 3 + k a 2 + k is equal to 2 0 . ⟹ 4 ( 2 k 2 ) 2 k 3 + k ( 2 k 2 ) 2 + k = 2 0 ⟹ 2 k + 2 k + k = 2 0 ⟹ k = 1 0
Let the coordinates of P be P ( p , k p 2 ) and let the coordinates of Q be Q ( q , k q 2 ) .
The slope of the tangent at P on y = k 1 x 2 is k 2 p and the slope of the normal at P is − 2 p k , making the equation of the normal y = − 2 p k ( x − p ) + k p 2 .
Since Q ( q , k q 2 ) is on the normal as well, k q 2 = − 2 p k ( q − p ) + k p 2 , which solves to q = − p − 2 p k 2 , so that the y -coordinate of Q is k q 2 = k p 2 + k + 4 p 2 k 3 .
By the AM-GM inequality, k p 2 + 4 p 2 k 3 ≥ 2 k p 2 ⋅ 4 p 2 k 3 = k , so k p 2 + k + 4 p 2 k 3 ≥ k + k = 2 k , which means the lowest possible y -coordinate of Q is 2 k .
Therefore, 2 k = 2 0 , and k = 1 0 .
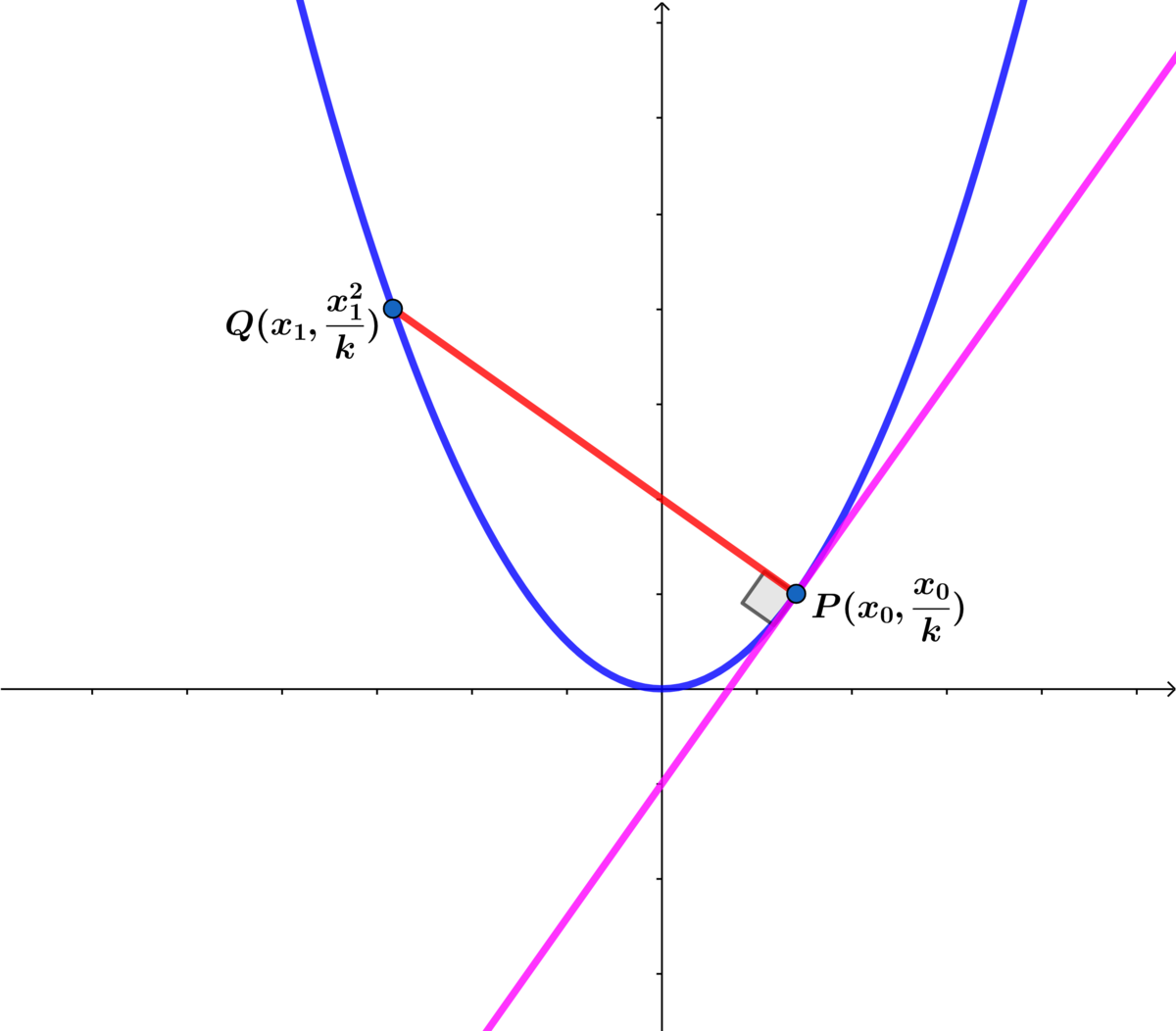
y 0 2 = k x 0 2 ⟹ y 0 ′ = k 2 x 0 ⟹ m P Q = − 2 x 0 k
At P : y = − 2 x 0 k ( x − x 0 ) + k x 0 2
At Q : x 1 2 = − 2 x 0 k ( x 1 − x 0 ) + k x 0 2
⟹ ( 2 x 0 ) x 1 2 + k 2 x 1 − ( k 2 x 0 + 2 x 0 3 ) = 0 ⟹ x 1 = 4 x 0 k 2 ± ( k 2 + 4 x 0 2
For ( + ) x 1 = x 0 ∴ drop ( + ) and choose x 1 = 4 x 0 2 k 2 − x 0 ⟹ k x 1 2 = 4 x 0 2 k 3 + k + k x 0 2
Let g ( x 0 ) = 4 x 0 2 k 3 + k + k x 0 2 ⟹
P : ( x 0 , k x 0 2 ) and Q : ( − 2 x 0 k 2 − x 0 , g ( x 0 ) ) .
g ( x 0 ) = 4 x 0 2 k 3 + k + k x 0 2 ⟹ g ′ ( x 0 ) = 2 x 0 3 k 4 x 0 4 − k 4 = 0
⟹ x 0 = 2 k
and
( − 2 k < x 0 < 2 k ⟹ g ′ < 0 ) and ( x 0 > 2 k ⟹ g ′ > 0 ) ⟹ min occurs at x 0 = 2 k
⟹ g ( 2 k ) = 2 k = 2 0 ⟹ k = 1 0
The gradient of the curve at the point P ( k t , k t 2 ) is 2 t , so the equation of the normal to the curve at that point is
x + 2 t y = k t + 2 k t 3
and this curve meets the parabola at the point ( k s , k s 2 ) where k s + 2 k t s 2 k ( s − t ) ( 1 + 2 t ( s + t ) ) = k t + 2 k t 3 = 0 so the point Q ( k s , k s 2 ) is given by s = − t − 2 t 1 . The y -coordinate of Q is thus k ( t + 2 t 1 ) 2 = k ( t − 2 t 1 ) 2 + 2 k and so the smallest possible y -coordinate of Q is 2 k . Thus we deduce that k = 1 0 .