Parity Blue and Yellow

Geometry Level 3

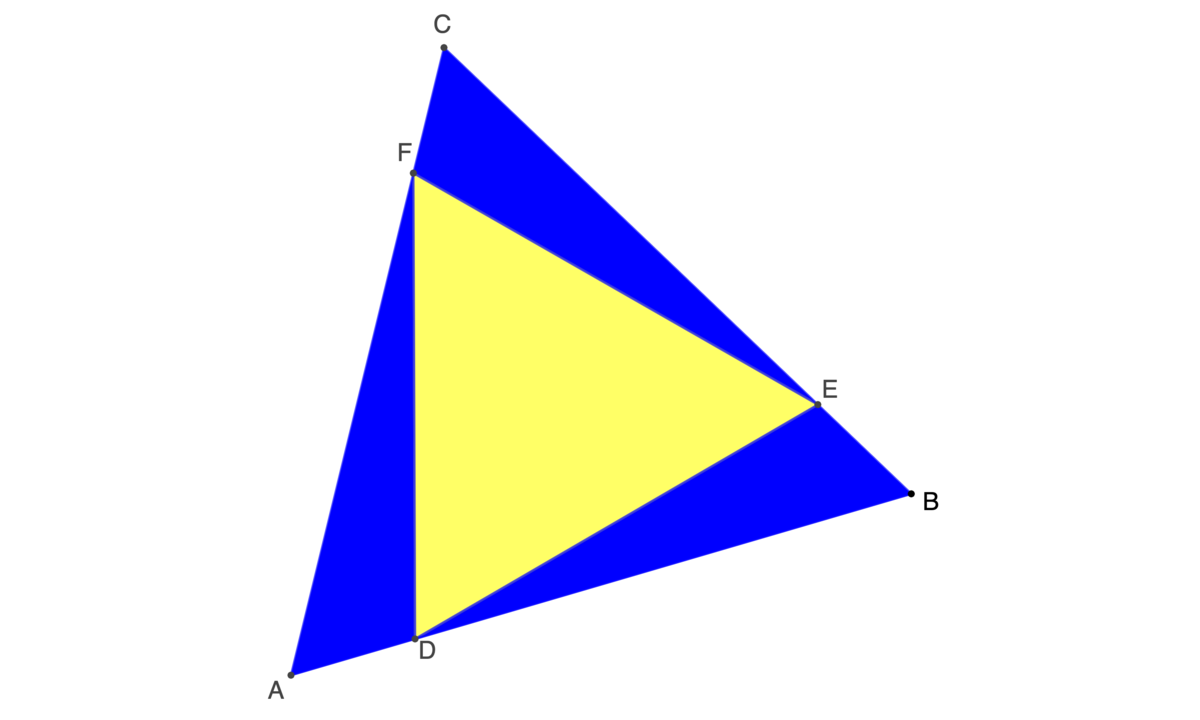
The figure shows a yellow equilateral triangle D E F DEF is inscribed inside a larger equilateral triangle A B C ABC with A B = 1 AB=1 .

If the blue area is equal to the yellow area, find A D = x AD =x . There are two values of x x . The smaller value of x x is equal A − A B \dfrac{A-\sqrt{A}}{B} , where A A and B B are integers and A A is square-free. Submit A + B A+B .

Inspiration - Blue or Yellow


The answer is 9.

Yuriy Kazakov by Yuriy Kazakov , 61, Russia

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Chew-Seong Cheong
May 24, 2021

When the blue area is equal to the yellow area, it means that the area of equilateral △ D E F \triangle DEF is half that of equilateral t r i a n g l e A B C triangle ABC . This means that the side length of △ D E F \triangle DEF , D E = 1 2 DE = \dfrac 1{\sqrt 2} . By cosine rule :

E B 2 + D B 2 − 2 E B ⋅ D B ⋅ cos ⁡ B = D E 2 Note that E B = A D = x x 2 + ( 1 − x ) 2 − 2 x ( 1 − x ) cos ⁡ 6 0 ∘ = 1 2 3 x 2 − 3 x + 1 2 = 0 x = 3 ± 9 − 6 6 = 3 − 3 6 Choosing the smaller value \begin{aligned} \blue{EB}^2 + DB^2 - 2\blue{EB} \cdot DB \cdot \cos B & = DE^2 & \small \blue{\text{Note that }EB = AD = x} \\ \blue x^2 + (1-x)^2 - 2 x(1-x) \cos 60^\circ & = \frac 12 \\ 3x^2 - 3x + \frac 12 & = 0 \\ x & = \frac {3\pm \sqrt{9-6}}6 \\ & = \frac {3-\sqrt 3}6 & \small \blue{\text{Choosing the smaller value}} \end{aligned}

The required answer A + B = 3 + 6 = 9 A+B = 3+6 = \boxed 9 .

3 Helpful 1 Interesting 4 Brilliant 0 Confused

Your latex math is broken. Hard to read :)

Richard Costen - 2 weeks, 2 days ago
Sathvik Acharya
May 23, 2021

Let x x denote the length of segment A D AD . So, we have, A D = B E = C F = x and A F = B D = C E = 1 − x AD=BE=CF=x \;\; \text{and}\;\; AF=BD=CE=1-x Using the Cosine Rule , in △ A F D , \triangle AFD, D F 2 = A D 2 + A F 2 − 2 ⋅ A D ⋅ A F ⋅ cos ⁡ ∠ D A F = x 2 + ( 1 − x ) 2 − 2 ⋅ x ⋅ ( 1 − x ) ⋅ cos ⁡ 6 0 ∘ = 3 x 2 − 3 x + 1 ∴ D F = F E = E D = 3 x 2 − 3 x + 1 \begin{aligned} DF^2&=AD^2+AF^2-2\cdot AD\cdot AF\cdot \cos \angle DAF\\ &=x^2+(1-x)^2-2\cdot x\cdot (1-x)\cdot \cos 60^{\circ} \\ &=3x^2-3x+1\\ \therefore \; DF&=FE=ED=\sqrt{3x^2-3x+1} \end{aligned} Yellow Area = area ( △ D E F ) = D F 2 ⋅ 3 4 = ( 3 x 2 − 3 x + 1 ) 3 4 Yellow Area + Blue Area = area ( △ A B C ) 2 ⋅ Yellow Area = A B 2 ⋅ 3 4 ( 3 x 2 − 3 x + 1 ) 3 2 = 3 4 6 x 2 − 6 x + 1 = 0 ∴ x = 3 ± 3 6 \begin{aligned} {\color{#CEBB00}\text{Yellow Area}}&=\text{area}(\triangle DEF) \\ &=DF^2\cdot \frac{\sqrt{3}}{4} \\ &=\frac{(3x^2-3x+1)\sqrt{3}}{4} \\ \\ {\color{#CEBB00}\text{Yellow Area}}+{\color{#0C6AC7}\text{Blue Area}}&=\text{area}(\triangle ABC) \\ 2\cdot {\color{#CEBB00}\text{Yellow Area}}&=AB^2\cdot \frac{\sqrt{3}}{4} \\ \frac{(3x^2-3x+1)\sqrt{3}}{2}&=\frac{\sqrt{3}}{4} \\ 6x^2-6x+1&=0 \\ \therefore \; x&=\frac{3\pm\sqrt{3}}{6} \\ \end{aligned} Therefore, x min ⁡ = 3 − 3 6 ⟹ A = 3 , B = 6 ⟹ A + B = 9 x_{\min}=\dfrac{3-\sqrt{3}}{6}\implies A=3,\;B=6\implies A+B=\boxed{9}

Alternative: Blue Area = 3 ⋅ area ( △ A D F ) = 3 ⋅ 1 2 ⋅ A D ⋅ A F ⋅ sin ⁡ ∠ A F D = 3 2 ⋅ x ⋅ ( 1 − x ) ⋅ sin ⁡ 6 0 ∘ = ( 3 x − 3 x 2 ) 3 4 \begin{aligned}{\color{#0C6AC7}\text{Blue Area}}&=3\cdot\text{area}(\triangle ADF) \\ &=3\cdot \frac{1}{2}\cdot AD\cdot AF\cdot \sin \angle AFD \\ &=\frac{3}{2}\cdot x\cdot (1-x)\cdot \sin 60^{\circ} \\ &=\frac{(3x-3x^2)\sqrt{3}}{4} \end{aligned} Since Yellow Area = Blue Area , {\color{#CEBB00}\text{Yellow Area}}={\color{#0C6AC7}\text{Blue Area}}, 3 x 2 − 3 x + 1 = 3 x − 3 x 2 ⟺ 6 x 2 − 6 x + 1 = 0 ⟺ x = 3 ± 3 6 3x^2-3x+1=3x-3x^2\;\Longleftrightarrow\; 6x^2-6x+1=0 \;\Longleftrightarrow\; x=\frac{3\pm\sqrt{3}}{6}

2 Helpful 1 Interesting 2 Brilliant 0 Confused

Note: A simple angle chase leads to ∠ A F D = ∠ B D E = ∠ C E F \angle AFD=\angle BDE=\angle CEF , which combined with ∠ A = ∠ B = ∠ C = 6 0 ∘ \angle A=\angle B=\angle C=60^{\circ} and D F = F E = E D DF=FE=ED implies that △ A D F ≅ △ C F E ≅ △ B D E \triangle ADF\cong \triangle CFE\cong \triangle BDE .

Sathvik Acharya - 2 weeks, 5 days ago
Saya Suka
May 24, 2021

AD = x = BE = CF so AF = 1 – FC = 1 – x.

1 blue area
= (1/2) × x × (1 – x) × sin 60°
= (Equal division of 3 blue area) × (Equal division of yellow-blue area) × (Full area)
= (1/3) × (1/2) × (1/2) × 1² × sin 60°


x (1 – x) = 1/6
x (x – 1) = –1/6
(x – 1/2)² = (1/2)² – (1/6) = 1/12
x = 1/2 ± 1/√12
= (√3 ± 1) / √12
= (3 ± √3) / 6

Answer = 3 + 6 = 9

1 Helpful 0 Interesting 1 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...