2002 Math OSK, Number 1: Transposing Evens
( 2 4 ) 8 ÷ ( 4 8 ) 2 = ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
31 solutions
(2^4)^8÷(4^8)^2= 2^32÷4^16= 1/2^16 what are you people doing? Two exponents next to each other such as (x^4)^8, you multiply the exponents. And then when dividing you subtract the eponent in the denominator from the exponent in the numerator. In this case 32-16, and then you divide your problem and the answer is 1/2^16
Log in to reply
You have to reduce the 4 to 2^2 first, then it becomes 32-32
thx.... v much
ya i forget it a little bit but am serprizaed to see answer
2^4 = 16 16^8 = 4.2949673e+009 4^8 = 65536 sqr(65536) = 4.2949673e+009 4.2949673e+009/4.2949673e+009 = 1
2^4 = 16 16^8 = 4.2949673+009 4^8 = 65536 (65536) = 4.2949673+009 4.2949673+009/4.2949673+009 = 1
Both gets cancelled when multiplies using laws of indices. Hence, we get 1 as our answer.
((2^4)^8)÷((4^2)^8) ((2^4)^8)÷((2^(2+2))^8) ((2^4)^8)÷((2^4)^8) =1
(2^4)^8=2^32 (4^8)^2=4^16=2^2^16=2^32
2^32-2^32 =2^1 =0
Just to add another solution to the pile. You are able to solve this problem utilizing lo g 2 and the basic understanding of exponents.
( 2 4 ) 8 = 2 8 ∗ 4 = 2 3 2
( 4 8 ) 2 = 4 8 ∗ 2 = 4 1 6
l o g 2 4 1 6 lo g 2 2 3 2
1 6 lo g 2 4 3 2 lo g 2 2
( 1 6 ∗ 2 ) ( 3 2 ∗ 1 )
3 2 3 2 = 1
Just observe that 4=2^2, so (2^4)^8=((2^2)^2)^8
work inside the parenthesis first . . . . . .
(2^4)^8 \divides (4^8)^2 =(2^4)^8 \divides (4^2)^8 =1 (Because 2^4 is the same as 4^2)
(2^4)^8÷ (4^8)^2
=2^32 ÷ 4^16
=(2^2)^16 ÷ 4^16
=4^16 ÷ 4^16
=1
[(2^4)^8=(16)^8]/ [(4^8)^2=(4^2)^8=(16)^8]
16^8/16^8=1
2^32/4^16=2^32-2^16-2^16=2^0=1
All exponents are multiplied together in the nominator and the denominator
Let,8 be =x,therefore:(2^4)^x ÷ (4^x)^2 ,2^4x ÷2^4x,then,just divide the two,an get 1
Something important for our youngs is to reinforce that we get "1" after cancellation of all numbers WHEN we are in process of multiplication / division... but we get "0" if we do the same in addition /subtraction.
(2^4)^8/(4^8)^2=(4^2)^8/(4^8)^2=4^16/4^16=1
All others have done brilliantly.. But what I've done is just see the order of the nbrs as 2,4,8 divided by the same nbr but order is changed 4,8,2 so i thought if the nbrs are same they must be equal to 1. ;-)
I am afraid that dosent work in all scenarios.
Take for example.
( 2 5 ) 8 = ( 8 5 ) 2
(2^4)^8 / (4^8)^2 = 2^32 / 4^16 Simplified, 2^32 / ((2^2)^8)^2 = 2^32 / 2^32 = 1
= [ (2^4)^8 ] / [ (4^8)^2 ] = [ (4^2)^8 ] / [ (4^8)^2 ] = Law of Exponents (Power raised to a power) --> 4^16 / 4^16 = 1 :)
2^4=4^2 So,by substituting one of them, it can be easily proven.
Moderator note:
Cute! You could have phrased your solution better like this:
Because 2 4 = 4 2 , then ( 2 4 ) 8 = ( 4 2 ) 8 = ( 4 8 ) 2 by properties of indices.
(2 * 2 * 2 * 2)^8 ÷ (4)^16 = ((4)^2)^8) ÷ (4)^16 = (4)^16 ÷ (4)^16 = 4^0 =1 OR (2)^4 ÷ (4)^2 = 16 ÷ 16 = 1 OR several other variations using the Laws of Exponents.
(2^4)^8 = 4294967296. (4^8)^2 = 4294967296
4294967296/4294967296 = 1
Moderator note:
It would be impractical to calculate large indices especially when one could easily simplify the work through the properties of indices.
You don't need to calculate them, this needed calculator or long time counting a needless number.
(2^4 )^8÷(4^8 )^2=(4^2 )^8÷(4^8 )^2=4^16÷4^16=4^(16-16)=4^0=1
2^4+8 ÷2^2+8+2= 2^12÷2^12= 1
Solve for the powers within parentheses. After that, you're all set. Both sides of the equation are equal. Divided, the answer is 1.
Cancel both 8 exponents and you'll get 2^4 / 4^2 which is 16/16=1
Honestly, I just canceled the ^8 s out and solved from 16/16 which equals 1
(2^4)^8 ÷ (4^8)^2 (2^4)^8 ÷ [4^2]^8 (2^4)^8 ÷ [(2×2)^2]^8 (2^4)^8 ÷ [(2^2)^2]^8 (2^4)^8 ÷ [2^2×2]^8 { BY LAW OF INDICES} (2^4)^8 ÷ [2^4]^8 =1
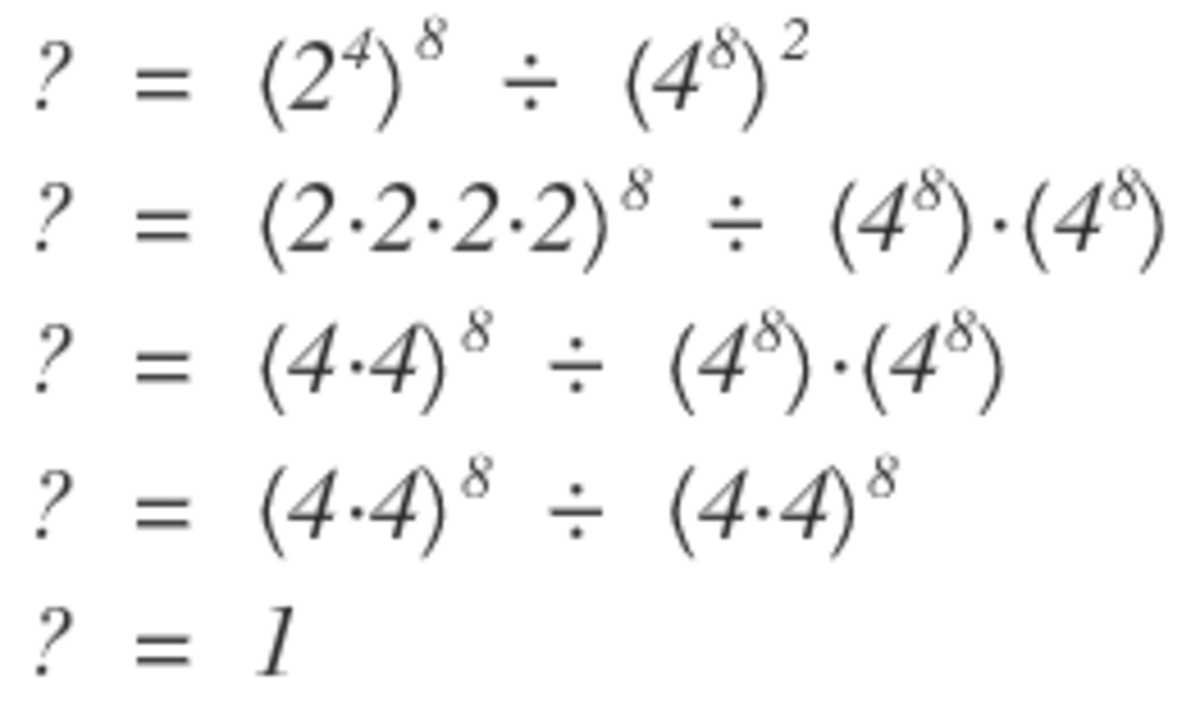
( 2 4 ) 8 ÷ ( 4 8 ) 2 = 2 3 2 ÷ ( 4 8 ) 2 = 2 3 2 ÷ ( ( 2 2 ) 8 ) 2 = 2 3 2 ÷ ( 2 1 6 ) 2 = 2 3 2 ÷ 2 3 2 = 1