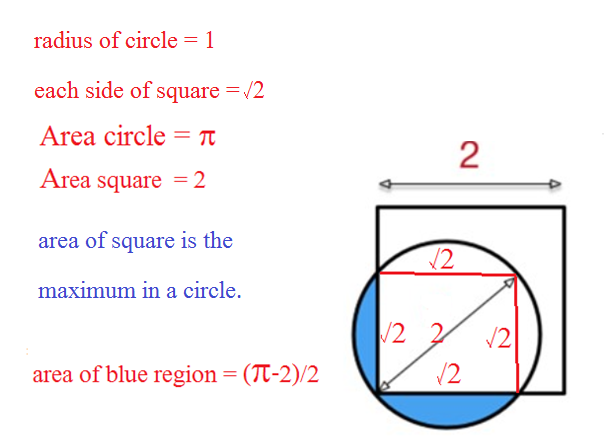
Part of circle outside square!

Let $A,B$ and $C$ be the points as shown below.

Because $\angle CBA$ represents an interior of a square, then $\angle CBA$ is a right angle, $90^\circ$ .

Draw a straight line from point $A$ to $C$ , we have a right triangle $ABC$ inscribed inside a circle. By Thales Theorem , the straight line $CA$ represents the diameter of the circle.

For simplicity sake, let $a$ and $b$ denote the lengths $AB$ and $BC$ respectively. Then by Pythagorean theorem , $a^2 + b^2 = 2^2 = 4$ , where $a,b> 0$ .

And the area of the shaded region can be found by finding the difference between the areas of the semicircle that passes through the points $C,B,A$ and the right triangle $CBA$ . Let $K$ denote the area of this shaded region, we have

$\ K = \dfrac12 \pi r^2 - \dfrac12 \cdot ab = \dfrac12 \pi \cdot \left( \dfrac22 \right)^2 - \dfrac12 ab = \dfrac12 (\pi - ab ).$

Since $a$ and $b$ represents two positive real numbers satisfying $a^2 + b^2 = 4$ as shown above, and we want to minimize $K =\dfrac12 (\pi - ab)$ , this motivates me to find a relationship between $a^2 + b^2$ and $ab$ , hence the use of power mean inequality :

$\begin{aligned} \sqrt{ \dfrac{a^2+b^2}2 } &\geq& \sqrt{ab} \\ \sqrt{\dfrac42} &\geq& \sqrt{ab} \\ 2 &\geq& ab \\ -ab &\geq& -2 \\ K = \dfrac{\pi-ab}2 &\geq& \dfrac{\pi-2}2 \\ \end{aligned}$

Thus the minimum value of $K$ (the area of the shaded region) is $\boxed{\dfrac{\pi - 2}2}$ , and it occurs when $a=b = \dfrac2{\sqrt2} = \sqrt2$ .

CA is a diameter (Because angle <CBA = 90º)

Blue area = Half Cercle - Triangle ABC = pi/2 - CA*h/2 = pi/2 - h, with h<=1

Blue area is minimum when when h=1, Minimum Blue Area = pi/2 -1