Partial Trial
Alice, Bob, and Cathy are on trial. Exactly one of them is guilty. They each make a statement:
- Alice says, "Bob is innocent!"
- Bob says, "Cathy is innocent!"
- Cathy says one of the three is guilty (maybe herself), but we don't hear who.
The judge knows who is guilty, and heard Cathy's statement. She says, "I could tell you what Cathy said and how many true statements were made, but you still wouldn't know who is guilty."
The judge adds, "I will tell you that the guilty party told the truth. Now if I told you how many true statements were made, you would know who is guilty."
Who is guilty?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
20 solutions
Correct answer = We don't know. 2 people could be telling the truth while one is lying. Judge says guilty party told the truth. Cathy could say she was guilty = Cathy told truth, Alice told Truth, Bob lied (Cathy did it). Cathy said Bob was guilty = Cathy told truth, Alice lied, Bob told truth (Bob did it) OR Cathy lied, Alice told truth, Bob told truth (Alice did it).
Log in to reply
The judge did say in his second statement that if he told us how many true statements were made we would know who did it. because the 2 true statements doesn't give a definitive answer there must only be one true statement as with 1 true statement we know who did it.
I don't get it...
See .Cathy said who is guilty. & if judge told you what Cathy said, u still don't know who is guilty. Means Cathy is 100% lying.
Now case1: Two truth.& guilty guys says truth. Meaning Alice is guilty.coz he says bob is innocent which must be true & Cathy is lying.
& case 2: one truth means Alice is wrong & innocent & bob is guilty. Coz bob says Cathy is innocent, which is true.
Both can be correct answer...how can u deduce to one ? Please explain
Log in to reply
You're probably not going to see this, but it might help others who are confused.
I believe case two to be the correct answer, as that was my answer. Case 1 would not work because if Cathy is lying and the others are telling the truth, then everyone is innocent.
Proof:
Alice: Bob is innocent (truth/ supposedly guilty)
Bob: Cathy is innocent (truth)
Now if Cathy accuses that Alice is guilty (we know Cathy always lies) then Alice would be actually be innocent (but someone must be guilty!). If Cathy accused herself or Bob, no one would know if Alice is guilty or innocent as no one would say anything about her (so you could not be certain that she's guilty or not, and the question says you should be certain)
Therefore only Case #2 works.
Very sufficient - love it!
I'm so dumb..Solved the whole of it correctly but clicked on the Wrong option...Feel like Hanging myself..BTW Good Question Maggie "DIDI"..Didi in Hindi means "Elder Sister" for your Knowledge..Hahahaha.. ;)
I did not understand. Please explain in detail.
Log in to reply
Essentially, all I did was check cases. These cases were the number of true statements. I eliminated the case of 0 and 3 and then focused in on the case of 1 , which turned out to be sufficient.
If Bob was the only one telling the truth, then Cathy lied about one of them is guilty. This is a contradiction.
Log in to reply
Yes...but no one say Cathie is telling truth. & judge says u don't know who is guilty after knowing Cathy statement...means Cathie is 100% wrong
Cathy didn't just say "one of them is guilty," she stated that a specific person is guilty.
Wow cool solution! I suddenly understand this question
When you check if Bob is guilty, don't you have to depend on what Cathy said? If Cathy said that Bob is guilty, then this would not work out, as you would have 2 true statements when there should only be one. From the question, I assumed the second statement meant that if the judge ONLY told that the guilty person told the truth and the number of true statements, WITHOUT telling what Cathy said, you would know who is guilty. Therefore, unless you know what Cathy said, then you cannot assume that Bob was guilty in this case. Do I not understand something? Please help.
Wonderful explanation....kudos!
I don't fully understand OP's solution, but I arrived at the same answer with a different method, so I'm going to piggyback on OP's comment so others can see (hope you don't mind, OP).
The answer must be derived from knowing the number of true statements, so we must find a case with an exclusive number of true statements (i.e. If there are two cases with 2 true statements, then neither case is the answer because we cannot distinguish between them).
Without any conditions (the judge's statements), there can be one case of 3 true statements, two cases of 2 true statements, three cases of 1 true statements, and none with 0 true statements. Since there is only one case with 3 true statements, then that's the case we want, and that case happens to make Alice the guilty party. In this case, Cathy must accuse Alice to satisfy 3 true statements, but the judge says Cathy's statement won't help us know who's guilty, which means Cathy's statement falls within a case without an exclusive number of true statements, so we cannot consider this exclusive case of 3 true statements and Alice is innocent.
If Alice is innocent, then Bill or Cathy must be guilty.
If Bill is guilty and Cathy accuses him, that's 2 true statements. If she accuses herself, then that's 1 true statement.
If Cathy is guilty and she accuses Bill, that's 0 true statements and that contradicts the judge. If she accuses herself, then that's 1 true statement.
Here we have one case of 2 true statements and two cases of 1 true statement. If the judge tells us there is only 1 true statement, then we cannot know for sure who is guilty. Since the judge says we can know for sure who is guilty from the number of true statements, then it must be the exclusive case of 2 true statements.
Bill is guilty.
I still don't understand who did Cathy say was the guilty one.
Now, I will explain why the assumption of 2 true statements doesn't leave us with any valid conclusion.
(a) Judge states: "I could tell you what Cathy said and how many true statements were made, but you still wouldn't know who is guilty." We could have - Hypothesis 1 - Bob and Alice said the truth - Alice is guilty. - Hypothesis 2 - Bob and Cathy said the truth - Bob is guilty. - Hypothesis 3 - Alice and Cathy said the truth - Impossible. This leaves us with a doubt, confirming the judge's statement. Remember, we still don't have the premise that the guilty party told the truth to check between the 2 valid hypothesis.
(b) Judge states: "I will tell you that the guilty party told the truth. Now if I told you how many true statements were made, you would know who is guilty." AND adds "There were 2 true statements". As we do not know who Cathy said was guilty, we can deduct that without the information about who Cathy said was guilty we can only evaluate the truthfulness of the statements of Bob and Alice. So: - Hypothesis 1 - Bob and Alice said the truth - Alice is guilty. - Hypothesis 2 - Bob and Cathy said the truth - Alice was lying so Bob is guilty. - Hypothesis 3 - Alice and Cathy said the truth - Bob was lying so Cathy is guilty. Anyone could be guilty.
This is why the solution can only be achieved if we assume that there was only 1 true statement.
I will make a table. Four row and three columns
In each cell, type in order, T or F, and the number of true. Use CAPITAL if the speaker is telling the truth For example, if Cathy says ALICE is Guilty, and Alice IS guilty, then Alice told the truth, Bob told the truth, and Cathy told the truth. So we have "T t t 4"
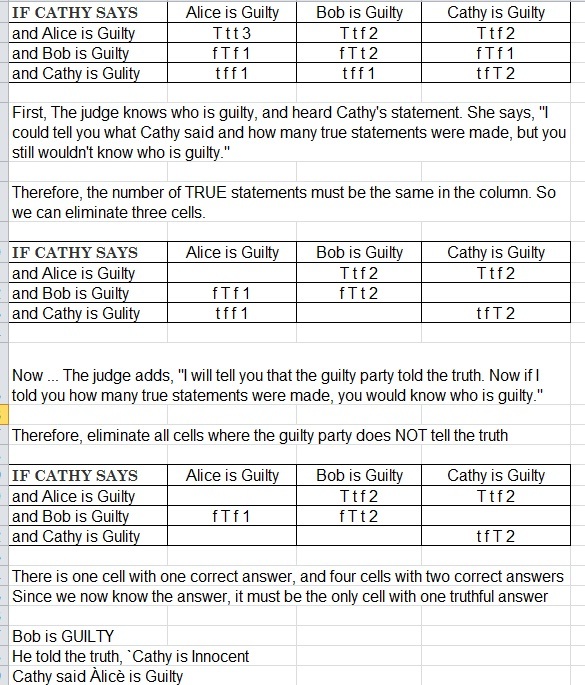
Clear solution, thank you!
Great solution! I thought myself in circles with this one for awhile and still got it wrong.
Its rather simple. The judge tell us that if we knew how many true statements were made we would know who is guilty, so there are three possibilities, one true statement, two true statements and three true statements. One has to be true atleast because cathy says that one of us is guilty which is an established fact. We know for sure that one of the three is guilty so we can conclude that cathy is telling the truth for sure. So considering the case of only one true statement, which must be only Cathy’s statement, meaning bob and alice are lying. According to this we have two guilty parties which cant be possible since there is only one. Now considering three true statements, this would mean that alice is guilty. So if there were three true statements judge wouldn’t have said that “ Number of true statements isn’t enough to find the guilty person’’ so we are left with the only possibility that there are two true statements. Judge adds that if he tells us that the guilty party told the truth we would know who is guilty. So starting with alice, if she was guilty that would mean she is telling the truth and cathy is telling the truth as well, which leaves us with bob telling a lie. Hence it can be concluded that alice and cathy are guilty which is again impossible. So one thing is for sure that Alice is not guilty. It leaves us with bob and cathy. Lets say cathy is guilty, that would mean either (cathy alice) or (cathy bob) are telling the truth since there are atleast two true statements. If (cathy alice) are telling the truth then cathy is indeed guilty but if (cathy bob) are telling the truth it would mean cathy and bob are guilty which is not possible. So here is the important bit, if cathy was guilty then judge’s information must have been enough to confirm it, since it contradicts with( cathy bob) telling the truth we can conclude that cathy is not guilty. Because if she was we would know from the information given by the judge. So alice is out and cathy is out. Leaving us with “ BOB” so bob is guilty which is confirmed as well. If bob is guilty then he and cathy are telling the truth which fits perfectly.
Just the way I did it myself.
First of all, the things we need to consider in this problem are 1. how many truthful statements were made,2. who cathy said was guilty and 3. the fact that knowing that the guilty person told the truth allows us to eliminate all but one suspect (which means that not knowing this, there must be at least 2 suspects). We know that there must be at least 1 or 2 truthful statements (see Ryan's explanation for why 0 and 3 truthful statements do not work)., so now all we need to do is try each remaining combination and find the only one that works to solve the problem. Lets start with the assumption that there are 2 truthful statements. Furthermore, lets assume that cathy said that alice is guilty. Given these assumptions, we now need to figure out who are suspects. We do so by seeing who could be guilty.
lets start with alice. if alice were guilty then that means that bob and cathy are innocent which means that everyone told the truth (remember that we are going under the assumption that cathy said that alice is guilty). Under our assumptions, one person must be lying which is not the case, therefor if there are 2 truthful statements and cathy said that alice is guilty, then alice must be innocent. Now lets check out bob. if bob is guilty then both alice and cathy lied, which does not meat with our assumptions (of 2 truthful statements), so we can eliminate that possibility. Now lets check out cathy. If cathy is guilty then bob and cathy are lying. Again, this does not work with the assumptions, making her innocent with the current assumptions. Since not all 3 people cannot be innocent, and under the current assumptions they would be, the assumptions are wrong.
Knowing that, lets try the assumption that cathy said that bob was guilty and keep the 2 truthful statements assumptions. could alice be guilty? if so, both alice and bob would be telling the truth while cathy would have lied. this works with our assumptions, making alice a suspect under the current assumptions. could bob be guilty? if so, then both bob and cathy are telling the truth and alice is lying. this also works with our current assumptions making bob a suspect. could cathy be guilty? if so, then both bob and cathy lied which goes against the assumptions, making that impossible with these assumptions.
Now that we have 2 suspects, we need to go back to the 3rd variable, the fact that knowing that the guilty person told the truth would let us know who is guilty. if alice is guilty, she must be telling the truth, keeping her as a suspect. furthermore, if bob were guilty, he must be telling the truth, keeping him as a suspect. since the additional information that the guilty person told the truth did not eliminate 1 suspect and leave us with just 1 suspect (the guilty person), the assumptions must be wrong.
Now lets try 2 truthful statements and cathy saying that cathy is guilty. could alice be guilty? if so, then both alice and bob are the truth and cathy is lying. this matches with our assumptions making alice a suspect. could bob be guilty? if so, then both cathy and alice would be lying which goes against our assumptions, making bob innocent with our current assumptions. could cathy be guilty? if so, then both alice and cathy would be telling the truth and bob would be lying, which matches with our predictions.
Again, we have 2 suspects and, therefore, need to go to the 3rd variable (see paragraph 1 for what that variable is). if alice is guilty, then she must be telling the truth, leaving her as a suspect. the same also goes for cathy. again, we still have 2 suspects when we should only have 1, making the current assumptions wrong.
By now we have determined that there cannot be 2 truthful statements, as we have tried every possibility given that there were 2 truthful statements (cathy saying that alice was guilty, that bob was guilty, and that cathy was guilty). this means that there must be exactly 1 truthful statement.
Given that there is 1 truthful statement, lets now go back to assuming that cathy said that alice is guilty. could alice be guilty? if so then all 3 statements would be true, which does not work with the current assumptions, making alice innocent with them. could bob be guilty? if so then both alice and cathy are lying, while bob is telling the truth. this matches the assumptions, making bob a suspect. could cathy be guilty? if so then both bob and cathy would be lying while alice would be telling the truth. this matches our assumptions, making cathy a suspect.
Now that we got another set of 2 suspects, lets go back to the third variable. (see paragraph 1 for what that variable is). if bob is guilty, then he must be telling the truth, keeping him as a suspect. however, if cathy were guilty, she must be lying, not telling the truth, eliminating her as a suspect. this leaves only bob as a suspect, making him the guilty person (as it satisfies all 3 variables).
Going on, you would find that with the assumption that there is 1 truthful statement and that cathy said that bob is guilty, only one person (cathy) would work with the assumptions (and there must be at least 2 suspects in order for the 3rd variable to be a factor), making that assumption not work. if you were to assume that there is 1 truthful statement and that cathy said that cathy is guilty, you would also only have one suspect (bob), making that assumption not work. finally, after this, there are no more assumptions, leaving the only assumption that works to be the correct assumption and leaving bob to be the guilty person.
P.S. this is the first solution guide i have ever written, so please excuse any minor mistakes it might have.
Woah! very detailed. Worth reading!
You forgot to consider in the begging of your logical thought that it's sure that cathy is lying.
very good explanation, well done ;)
Cathey said, "Alice is guilty" Two statements were true. If we didn't know That the guilty person will tell the truth- it could be either Alice or Bob. But under the condition of the guilty person telling the truth Alice can't be guilty since she's lying. So, Bob is guilty
I'm not brilliant at formatting but I'll try my best to explain how I got there. My eventual method was to more visually tabulate this information on a spreadsheet and colour in cells, but that isn't so translatable here. Throughout the solution I will use binary notation to indicate truth ( 1 ) or lie ( 0 ). Furthermore let the ordered set of truths/lies for A , B and C be notated as S x y . x tells us who Cathy says is guilty, and y tells us who was actually guilty.
Let's take all the various cases:
S A A = { 1 , 1 , 1 } S A B = { 0 , 1 , 0 } S A C = { 1 , 0 , 0 }
S B A = { 1 , 1 , 0 } S B B = { 0 , 1 , 1 } S B C = { 1 , 0 , 0 }
S C A = { 1 , 1 , 0 } S C B = { 0 , 1 , 0 } S C C = { 1 , 0 , 1 }
If the judge told us what Cathy said, we would be able to narrow the combination down to one of the three blocks. But the judge says that if they gave away how many statements were true, we still wouldn't know who is guilty. Therefore if the number of truths in a combination is unique within its row of combinations for which x is the same, it must be removed (otherwise the judge's initial statement would give it all away). Remaining:
S A B = { 0 , 1 , 0 } S A C = { 1 , 0 , 0 }
S B A = { 1 , 1 , 0 } S B B = { 0 , 1 , 1 }
S C A = { 1 , 1 , 0 } S C C = { 1 , 0 , 1 }
Now we are told that the guilty party told the truth. Therefore let's remove the combinations in which the guilty party lied. Remaining:
S A B = { 0 , 1 , 0 } S B A = { 1 , 1 , 0 } S B B = { 0 , 1 , 1 } S C A = { 1 , 1 , 0 } S C C = { 1 , 0 , 1 }
We are told that in this list of remaining solutions, being given the number of truths told will give the game away. Therefore there must be a number of truths which is unique to only one combination in this list. The correct combination is S_AB. In this case, Bob is the guilty person.
First of all: we cannot have 0 truthful statements: Alice and Bob can't be lying at the same time, or we would have more than one guilty person. Also, having 3 truths means that Alice is guilty, which puts in check the first statement of the judge. So, there can be only 1 or 2 truthful statements.
Cathy can say that either Alice, Bob or herself is guilty. Then we have 3 cases: each one for one number of supposed truthful statements ( 1 ; 2 ) and one person being accused by Cathy ( A ; B ; C ) .
Also, for each case, there will be subcases representing the order in which truths and lies associate with the persons, by alphabetical order of their names. Let's say Alice lies, Bob tells the truth and Cathy lies; so, we have L i e , T r u t h , L i e , or L T L .
For 1 truth we have L T L or T L L ( L L T is disconsidered because Alice and Bob can't be lying at the same time) and T T L , T L T and L L T for 2 truths. That gives us a total of 1 5 subcases.
Let's analize the case in which there is 1 truth and Cathy accuses Alice ( A 1 ):
1st subcase: L T L
A lies: B is guilty, or A l = B g
B tells the truth: C is innocent, or B t = C i
C lies: A is innocent, or C l = A i
In this subcase Bob is guilty and is telling the truth (or B t ).
2nd subcase: T L L
A t = B i
B l = C g
C l = C i
In this subcase Cathy is guilty but she's NOT telling the truth (or C l ).
Then, for case A 1 , either Bob is guilty and is telling the truth, or Cathy is guilty but she is lying. Or, lets's say, A 1 = ( B t + C l ) .
If we analyze all cases that way, we will see that some cases gave us two possible different guilty persons, some just one possible guilt person, and some are simply illogical (the statements contradict themselves).
By the fisrt statement of the judge, we can only consider the cases in which we have at least two possible guilty persons. Those are three in total: A 1 = ( B t + C l ) ; B 2 = ( A t + B t ) ; and C 2 = ( A t + C t ) .
By the judge's second statement, we can say that case A 1 resumes to A 1 = ( B t ) , because the guilty person is telling the truth (if case A 1 is real, then Cathy coudn't be guilty because she's lying); we can also say that knowing the number of truths give us the guilty person; for 1 truth there is only A 1 , but for 2 truths there are both B 2 and C 2 and we still wouldn't know which one of them is the real case. Then, only A 1 = ( B t ) can be true, so Bob is guilty.
Also, if either B 2 or C 2 were true, in each one of them there are two possible guilty persons telling the truth, which also too is not sufficient for determining which of them is guilty. This as well would lead to A 1 = ( B t ) being the only real possibility. Bob is going to the jail anyway.
Note: the "logical" notation i used here isn't "logical" or formal by any means. I invented it just beacause i didn' want to type a thousand times the same things like "Bob is guilty and is telling the truth, or Cathy is guilty but blah blah blah". Also reading this answer would be 300x more boring than it already is.
Because the judge originally says "I could tell you what Cathy said and how many true statements were made, but you still wouldn't know who is guilty." I decided to go through what Cathy could say and find the similar amount of truths. Then looking at those cases, finding out if the guilty person might have told the truth.
Case 1: Cathy said Alice was guilty.
If Alice was guilty, Alice, Bob and Cathy would all be telling the truth. 3 truths. If Bob was guilty, only Bob would be telling the truth. 1 truth. If Cathy was guilty, only Alice would be telling the truth. 1 truth.
So, if Cathy said that Alice was guilty, there would have to be only 1 truth told, or I'd be able to say who was guilty.
Bob would have to be the guilty person as he was the only person that told the truth when he was assumed guilty.
Case 2: Cathy said Bob was guilty.
If Alice was guilty, Alice and Bob would be telling the truth. 2 truths. If Bob was guilty, Bob and Cathy would be telling the truth. 2 truths. If Cathy was guilty, only Alice would be telling the truth. 1 truth.
So, if Cathy said that Bob was guilty, there would have to be 2 truths told, or I'd be able to say who was guilty.
Even when knowing that 2 truths were told, both Alice and Bob told the truth when they were guilty.
Case 3: Cathy says that she is guilty.
If Alice was guilty, Alice and Bob would be telling the truth. 2 truths. If Bob was guilty, only Bob would be telling the truth. 1 truth. If Cathy was guilty, Alice and Cathy would be telling the truth. 2 truths.
So, if Cathy said that she was guilty, there would have to be 2 truths told, or I'd be able to say who was guilty.
Even when knowing that 2 truths were told, both Alice and Cathy told the truth when they were guilty.
Conclusion: Since we were eventually told "I will tell you that the guilty party told the truth. Now if I told you how many true statements were made, you would know who is guilty." I could look back and see that Case 1, Bob being guilty, was the only case that knowing about the number of true statements and guilty truth confession could have logically told me which was guilty.
So it kills me to say that Bob (the only male in the room) is guilty
Pay attention to these points
1) ambiguity of guilt even after some revealing hints,
2) the only guilty party told the truth (NOT ONLY THE, but the only = the sole, so those innocent people could have told the truth too, but not necessarily so), and
3) distinctive number of true statement(s)
To start, we have
A saying IB
and
B saying IC (A for Alice, B for Bob, C for Cathy, I for innocent, G for guilty).
What A & B said doesn't really corroborate with each other, but both can't be lying simultaneously as we cannot have more than 1 guilty party.
From #2, we have at least 1 truth out of the 3.
From #1, we can't have gotten the truth from all the suspects (if the judge had told you 3 is the number of true statements, then the extra hints of #2 & #3 would be rendered irrelevant and unnecessary + #1 as untrue, as there's only 1 way for that case to happen by C accusing GA after 2 assumed truths of IB + IC).
So, we're left with 1 or 2 true statements to leave some sort of ambiguity remaining behind before we extinguish them in the end.
Let's assume the 3 suspects to be guilty, 1 by 1.
GA would tell the truth with IB. IB can't be wrong with IC, thus a 2nd truth there. As already explained before, IC can't accuse GA for the 3rd one, but no matter what she said (GB or GC), we have 2 max truths attained in this case.
Conclusion(s) : 2 possible cases, both 2 truths, IC accused GB or GC, both innocents.
Now, GB would tell the truth with IC. IA on the other hand lied with her claiming IB. Depending on what IC said, the number of true statements in this case is 1 OR 2.
Conclusion(s) : 3 possible cases, IC falsely accused GA or GC (1 truth for both cases), or IC rightly accused GB (2 truth for this case).
Lastly, GC must tell the truth (as per hint #2) by incriminating herself as GC. IA added on the 2nd one and IB who maintained IC lied in this case. So 2 truths here.
Conclusion(s) : 1 solely possible case, GC truthfully admitted being GC by herself (2 truths in this case).
We see that for the 1st & 3rd case, both can't fulfill hint #3, so we can finally deduce that it really was GB with IC falsely accusing GA.
{ The judge knows who is guilty, and heard Cathy's statement. She says, "I could tell you what Cathy said and how many true statements were made, but you still wouldn't know who is guilty."
The judge adds, "I will tell you that the guilty party told the truth. Now if I told you how many true statements were made, you would know who is guilty." }
| Accused / Guilty | Alice | Bob | Cathy | Note 1 |
| Alice | TTT3 | TTF2 | TTF2 | 3 is the odd one out among (3,1,1) |
| Bob | FTF1 | FTT2 | FTF1 | 1 is the odd one out among (2,1,2) |
| Cathy | TFF1 | TFF1 | TFT2 | 1 is the odd one out among (2,2,1) |
| Accused / Guilty | Alice | Bob | Cathy | Note 2 |
| Alice | X | TTF2 | TTF2 | Alice is consistently truthful in this row |
| Bob | FTF1 | FTT2 | X | Bob is consistently truthful in this row |
| Cathy | TFF1 | X | TFT2 | guilty Cathy accusing an innocent Alice just didn't happen (according to the judge) |
| Accused / Guilty | Alice | Bob | Cathy | Note 3 |
| Alice | X | TTF2 | TTF2 | |
| Bob | FTF1 | FTT2 | X | Bob's the only one with a case of 1 true statement made |
| Cathy | X | X | TFT2 |
My unedited thoughts (I bet it can get cleaned up and shortened):
It's impossible for both Alice and Bob to lie because two people would be guilty. So there must be at least one true statement coming from either or. If the judge told us that 2 statements are true, then we would know who is guilty because either both Alice and Bob exonerate 2 people, leaving the third one as the guilty one, or one of them exonerates and the other one points to the guilty one. This happens regardless of what Cathy says. Then exactly 1 statement made is true and it's not what Cathy said (at this point we know that either Bob or Cathy is guilty). If Cathy says that Bob is guilty, then he is innocent and therefore Alice told the truth, meaning, Bob lied and we would know. According to the judge, this would not happen. If Cathy says that she is guilty, then Bob told the truth, Alice lied, and therefore Bob would be guilty. Again, this would not happen. So Cathy said that Alice is guilty (I think this part is irrelevant). But then since Alice is innocent, she did not told the truth (exactly one statement is true and was uttered by the guilty party). Then Bob told the truth and he is the guilty one.
the creator was a 25 yr old female. Of course the only man would be the guilty one.
If 3 true statements are made, then both Bob and Cathy are innocent, and Alice is guilty. This is a contradiction, since we should be unable to know who the guilty person is according to the judge.
If 0 true statements are made, then both Bob and Cathy are guilty. This is a contradiction, since only one person may be guilty.
If 2 true statements are made, then it cannot be from both Alice and Bob, for the same reason that 3 true statements cannot be made. If Bob and Cathy are telling the truth, then we know who is guilty, since Cathy says who they are. This is a contradiction. For this same reason, the two truth tellers cannot be both Alice and Cathy, since Cathy will tell us who it is. At no point can Cathy be telling the truth, since we will instantly know who it is.
If 1 true statement is made, then we know that the other two statements are false. If Alice tells the truth, then we know that when Bob says that Cathy is innocent, he is lying, and therefore we know that Cathy is guilty, which contradicts the judge's statement. The same logic applies to Bob. If we know Alice is lying, we know Bob is guilty. Again, if Cathy is telling the truth, then we automatically know who is guilty.
Neither 3, 2, 1, or 0 true statements can be made following the judge's statement. I feel like this was overlooked. Since the first statement the judge makes stands on its own, it has to be checked for validity before the second statement comes in. Even if the second statement fixes the issue with the first, it still remains that by the judge's own logic the puzzle cannot be solved. This line of reasoning is further enforced when the judge says "Now if I told you....", implying that knowing the guilty party was telling the truth matters. Again, the issue here is that regardless of how many statements are made, Cathy must be lying.
So, either 0 true statements are made, 2 true statements are made and they are from Alice and Bob, 1 true statement is made and it is from Alice, or 1 true statement is made and it is from Bob.
All of these tell us who is guilty, or are self-contradictions. The puzzle only seems to make sense if you ignore what the judge initially says and go right to the second statement. Of course, if Cathy is lying, she must be innocent. Which means Bob is telling the truth, and is therefore guilty. A side note is that Cathy couldn't name Bob or she would be telling the truth, which we know cannot happen.
So, this means that Bob told the truth. Going back to what the judge said; if "you wouldn't know who is guilty" is another way of saying "the puzzle results in a contradiction", then sure. My only problem is that if that was the case, you could just as easily say that the guilty person told the truth, and the puzzle would be the same, just with fewer pointless if-thens.
"Exactly one of them is guilty and the guilty party told the truth." Now, Cathy says one of them is guilty but doent tells the name of the person (but she knows the name). That means she wants to save the one who is guilty. And in turn who is defending her - Bob. It means he is the one who is guilty.
Before I get on with my thought process, the key to my solution was the judge's statement: The guilty party tells the truth
My solution process for this was quite short. Cathy is ruled out from being guilty because if she'd told the truth, she would have said it's her, but the judge's first statement contradicts that ("I could tell you what Cathy said ... but you still wouldn't know who is guilty"). This makes Cathy innocent, and that leaves Bob and Alice. Back to the key statement above: The guilty party tells the truth . Bob said Cathy is innocent, which is the truth, so Bob is the guilty party.
Exactly one of A,B,C is guilty. 3 statements made, true or false. Truth: 1 Lie: 0
A B C
0 0 0 0 B and C are guilty. zero truths. C lied A
1 0 0 1 B and C are guilty. one truth. C named A and B
2 0 1 0 B is guilty. 1 truth. C lied A or C
3 0 1 1 B is guilty. 2 truths. C named B
4 1 0 0 C is guilty. 1 truth. C lied A or B
5 1 0 1 C is guilty. 2 truths. C named C
6 1 1 0 A is guilty. 2 truths. C lied B or C
7 1 1 1 A is guilty. 3 truths. C named A
First strike options 0 and 1. There is only one guilty party, so A or B needs to tell the truth.
"I could tell you what Cathy said and how many true statements were made, but you still wouldn't know who is guilty."
So, the correct answer cannot be option 7, because then we would not need the extra clues.
"I will tell you that the guilty party told the truth. "
Now we can strike option 4, as there the guilty party was lying.
Options remaining:
if there is one truth: option 2 is the one.
if there are two truths: options 3, 5 and 6 can be possible.
In case of option 6, C lied, either B or C. In case of option 3 and 5, she told the truth, either B or C.
So we cannot know which one is guilty if there are two truths. The smart judge knows this and would have added more clues, but did not. So it has to be option 2: B is guilty.
Since Alice and Bob's statements are fixed, we need only consider them in relation to Cathy's testimony.
Thus, (shorthand, Alice says Bob is innocent = A -> B.I.):
- Possible testimony #1: A -> B.I, B -> C.I and C -> A.G
- Possible testimony #2: A -> B.I, B -> C.I and C -> B.G
- Possible testimony #3: A -> B.I, B -> C.I and C -> C.G
- PT #1 (1 truth by Alice): B.I, C.G and A.I which implies C.G (but C is lying bc she lied about A's guilt)
- PT #1 (1 truth by Bob): B.G, C.I and A.I which implies B.G (B is truthful bc he truthfully asserted C's innocence)
- PT #1 (1 truth by Cathy): B.G, C.G and A.I which implies two guilty individuals (contradiction)
So you see that with 1 truth there are two possible guilty individuals, thus fulfilling the judge's proclamation that without knowing the truthfulness of the guilty party, we will not know who is guilty. Without that info, we would not know whether C.G or B.G. This ambiguity is a necessary component as we will see shortly.
- PT #1 (2 truths by Alice & Bob): B.I, C.I and A.I which implies no one's guilty (contradiction)
- PT #1 (2 truths by Alice & Cathy): B.I, C.G and A.G which implies two guilty individuals (contradiction)
- PT #1 (2 truths by Cathy & Bob): B.G, C.I and A.G which implies two guilty individuals (contradiction)
There are no scenarios where we can deduce guilt given this PT and 2 truths.
- PT #1 (3 truths by Alice & Bob & Cathy): B.I, C.I and A.G which implies A.G (A is truthful bc she truthfully asserted B's innocence)
But uh oh, didn't we say it was B.G earlier? Yes, we did! So which is it? B.G or A.G?
Remember, the problem states that the judge told us,"I could tell you what Cathy said and how many true statements were made, but you still wouldn't know who is guilty." Well, if that's the case, then we shouldn't know who is guilty based off of number of truth statements and Cathy's testimony alone. But we DO know that! Three truths with C -> A.G implies A.G. We can deduce that even without the judge offering additional information regarding the guilty individual's truthfulness. Compare that to the 1 truth statements where we had two possible guilty verdicts UNTIL we examined them for truthfulness. Therefore, we can conclude from our PT #1 (1 truth) statements that BOB IS GUILTY !
Trying this with the other PT's:
Recall,
Possible testimony #2: A -> B.I, B -> C.I and C -> B.G
- PT #2 (1 truth by Alice): B.I, C.G and B.I which implies C.G (but C is lying bc she lied about B's guilt)
- PT #2 (1 truth by Bob): B.G, C.I and B.I which implies both B.G and B.I (contradiction)
- PT #2 (1 truth by Cathy): B.G, C.G and B.G which implies two guilty individuals (contradiction)
This is another scenario where we would deduce C.G if we didn't have the additional information regarding truthfulness. Since the judge said, "I could tell you what Cathy said and how many true statements were made, but you still wouldn't know who is guilty," we know that C.G is not ambiguous enough. After all, we CAN deduce it without knowing the truthfulness of her testimony. However, knowing that the guilty party is truthful, while also knowing that Cathy is lying, we know that she can not be the guilty individual.
- PT #2 (2 truths by Alice & Bob): B.I, C.I and B.I which implies A.G (A is being truthful about B's innocence)
- PT #2 (2 truths by Alice & Cathy): B.I, C.G and B.G which implies two guilty individuals (contradiction)
- PT #2 (2 truths by Bob & Cathy): B.G, C.I and B.G which implies B.G (B is being truthful about C's innocence)
In this case (PT #2 with 2 truths), we have two possible scenarios where an individual is both truthful and guilty. Therefore, this PT is inconclusive since even with all the information at our disposal, we still can't deduce who is guilty.
- PT #2 (3 truths by Alice & Bob & Cathy): B.I, C.I and B.G which implies both B.G and B.I (contradiction)
Recall,
Possible testimony #3: A -> B.I, B -> C.I and C -> C.G
- PT #3 (1 truth by Alice): B.I, C.G and C.I which implies both C.I and C.G (contradiction)
- PT #3 (1 truth by Bob): B.G, C.I and C.I which implies B.G (B is being truthful about C's innocence)
- PT #3 (1 truth by Cathy): B.G, C.G and C.G which implies C.G (C is being truthful about her guilt)
Once again this scenario is inconclusive since we have two potential scenarios with a guilty individual being truthful.
- PT #3 (2 truths by Alice & Bob): B.I, C.I and C.I which implies A.G (A is being truthful about B's innocence)
- PT #3 (2 truths by Alice & Cathy): B.I, C.G and C.G which implies C.G (C is being truthful about her guilt)
- PT #3 (2 truths by Bob & Cathy): B.G, C.I and C.G which implies two guilty individuals (contradiction)
Once again, it's inconclusive.
- PT #3 (3 truths by Alice & Bob & Cathy): B.I, C.I and C.G which implies both C.I and C.G (contradiction)
Given that the judge says the guilty party told the truth and that there is only one guilty party, then there must only be 1 true statement (if there was more than 1 true statement, then there would be multiple guilty parties which contradicts the fact that there is only one guilty party). Alice's statement cannot be true since then Bob's statement would be A lie which would mean that Cathy is guilty; however Alice and Cathy cannot both be the guilty party, so Alice's statement must be false. Therefollows, Bob's statement must be truth since Alice's statement has been established as false which her statement translates into Bob being guilty which means Bob must say the truth. We know that Cathy's statement must be a lie, so she either said "Cathy is guilty" or "Alice is guilty." From all this, we can conclude that Bob is guilty.
I suppose this can be solved like this : since the judge said that knowing what Cathy told and the number of true statements wouldn't be enough to determine the guilty person this means that there should be at least one case in which we wouldn't have enough information to determine just one solution for who the criminal is and therefore , of course (by ordinary and pretty banal use of logic by it's simple use therefore) , that by what the judge tells us there must be a case where on the account of the first information presented would be more than one possible guilty person. Now we should understand firstly better why or how the solutions look like (since this understanding seem to be what we are lacking or we just have an incomplete grasp of it) so that there are more than one solution in order to determine what that case actually is and by this understand afterwards what the solution is. This approach leads in making our searching explicit enough since we can put the question pretty precise by these form : how should that case look like in order to remain consistent with the affirmations of the judge ? This would be what we may a little bit metaphorically (i should add) call "the order" of our strategy , our immediate approach towards the problem by which we should enter in the reason of it which may be called "meta-logical" by it's turning to the possibility of logic and use of reason and this should be seen at the level of explanation of this two things. I will add that i say this not just as a remark but in order to see (or think) of the solution of the problem in the terms of this "meta-logical" thinking turning in it's imprecision at the possibility of a deduction seeing it not by taking any individual cases but rather at a more abstract thinking which sees all this individual cases by what we can deduce from them. And now returning to the problem....
Trying to determine what the reason of this problem actually is observe that Alice says "Bob is innocent" (P1) and Bob says "Cathy is innocent"(P2) which means that if Cathy said that either Bob or Cathy are guilty this would contradict either P1 or P2 and therefore for this 2 cases we would have 2 contradicting propositions 1 of them being true and the other one false (without having importance for deducing this which is false and which is true) and by having this "invariant relationship" by knowing the truth values of the "composite" P1 and P2 we will have that we have one false statement and one true which means that we know the truth values of 2 statements out of the total of 3 told which implies that if we are told the number of true statements this would be sufficient to deduce the truth value of the last proposition. Since this proposition would be either P1 or P2 knowing it's truth value will tell us who is guilty and by this it would mean that if Cathy told that either Bob or Cathy is guilty on the grounds of what the judge would tell us we will have enough information to deduce who is the "guilty party" which contradicts the first affirmation of the judge which tells that on this same grounds we wouldn't know certainly who is guilty therefore meaning that this two can't be the actual case.
Now if Cathy says that Alice is the guilty person this wouldn't contradict any of the other 2 propositions and since this is also the only possible case left we should consider it closely. Here we can relate to the fact that for this case Cathy could have told the truth or not which would also imply like in the other situation some sort of relationship between the truth values of the composite made by the first two propositions P1 and P2. This last part of our reasoning is at least from how it appears to me a little bit more complicated but i think we can put it in the same abstract thinking like this : we can say that Alice , Bob and Cathy refer all of them to a different person than the person to which the other two speak of ( that is a proper interpretation for the fact that Alice speaks of Bob , Bob of Cathy and Cathy of Alice) in their statements which would mean that the truth value of Cathy's statement will affect in some way the truth value of the other two and determine somehow the number of true statements which we would know if the judge told us. Now one of this cases that in which Cathy tells the truth falls since if she tells the truth Alice is guilty and P1 and P2 (referring to different persons) must be both true also but in this case we would have a total of 3 true statements which would contradict what the judge told (that if we know the number of true statements and what Cathy told we wouldn't know who the guilty person is) since by being a total number of 3 statements Cathy's statement would also be true and by this last statement it would be sufficient to know who is the guilty person. We remain therefore with the case in which Cathy's statement is false which means that Alice is innocent and therefore that either Cathy or Bob is guilty. Yet since we know (by what the judge says) that the "guilty party told the truth" and Cathy's statement was determined to be false we can now deduce that Bob is the one who is guilty.
We could have simply taken the cases of course one by one but in that way the reason of the deductions (and this means more precisely the motives and formal way of arranging the thought of the way the deductions where presented and developed by their principle) wouldn't have appeared and it is in some way this reason into which we should try to go deeper until we understand it and in some way the entire topology it may be said of solutions. I'd like to say that what i did here isn't just "checking cases" and that no one who thinks logically even if he believes this or not solving this problem just "checked" the cases but rather arrived at the solution guided by a reason which motives were i hope at least a little bit more been presented more clearly and completely but this is a little bit another mater anyways.
This was my thinking when solving this. The key is the very beginning that states Exactly one person is guilty and the Judges statement saying that the guilty party is telling the truth, by default then only one statement can be true because only one person is guilty and they told the truth which means two statements are lies. Which brings me to Cathy's statement we don't know what Cathy said so that is our variable. Now lets look at all possibilities for Cathy's statement. First is Cathy saying she is innocent, if that were true then that would make Both hers and Bob's statement true so that eliminates that possibility because that would mean 2 people were guilty and only one can be. So we know she didn't say that. If she say's I'm guilty then both her statement and Alice's would be true(because Bob by default would be innocent). So we know she mentioned either Alice or Bob. If she say's Alice is innocent and told the truth she would be guilty but that would also make Alice's statement true because by default Bob would be innocent and two people can't be guilty) Same goes if she said Alice was guilty(Both Cathy and Bob would be telling the truth). So the only scenario is that Cathy lied and said that Alice was Innocent because that's the only scenario were the out come is not two people telling the truth and being Guilty. So now that we know Cathy Lied let's Look at Alice. Alice said that Bob was innocent if she is telling the truth then that means that Bob is telling the Truth and therefore two people are Guilty so you know she is lying. Process of elimination tells you then that Bob is Telling the Truth and is the guilty party, because if he is Lying that then means that Both Cathy's statement and Alice's Statements were true. Because by default both Alice and Bob would be innocent.
"I could tell you what Cathy said and how many true statements were made, but you still wouldn't know who is guilty" C gave us a statement of someone's guilt. If C said A did it (truthfully), then the other two statements are true and the Judge's hint is moot. If C said B did it truthfully, then the Judge is still self-contradicting (logic would lead to the guilty party if C told the truth in any scenario). "I will tell you that the guilty party told the truth. Now if I told you how many true statements were made, you would know who is guilty." Simply, C was innocent and wrongly accused someone (found from the first hint) and therefore B was telling the truth at least -- therefore, from the information we have, B is guilty.
from the judge's first statement , we have to ask ourselves a question " when could the judge tell us what Cathy said and number of the true statements and we still don't know the guilty one ? " if Cathy said " me " we have three options
1- the three statements are true , it cant be because bob said that she was innocent
2- two statements are true ,cant be because we could easily know the guilty ,will be Alice
3- one statement is true ,think about it , it can't be also
so Cathy is innocent, so bob is telling the truth and according to the second statement of the judge that the guilty is telling the truth then bob fits it but to make sure ,lets see what if Cathy said bob :
1- the three statements cant be true because either Cathy and Alice is lying
2- two statements are true , it fits well because we won't know the guilty even when we know what Cathy said and the number of the true statements ,so that's is the case we are looking for which fits the judge's first and second statement so bob is the guilty . sorry for my poor grammar, please correct me if I am wrong
I am puzzled from the problem and I shall briefly explain, since first the problem states that exactly one is guilty and that the judge gives the setting to make us solve and understand the problem of the guilty party, so however in my case I saw it better as below. Alice could be either guilty or innocent. Bob could be either guilty or innocent. Cathy is remained in doubt from the starting point in the problem since we should get one of them to be in the assumption of absolute guilt. So we turn to what the judge is stated; she says that she could tell us what Cathy stated. But remember what she could state something that could incriminate her or free her. If she states that Alice is guilty that could still fit the understanding in the problem that Bob and Cathy are now free an innocent. Because the judge knows who is guilty she says somehow we will get to find the guilty by adding teh guilty party told the truth so Alice stated Bob is innocent fits also this case.
So Bob and Cathy tell separate truths and even if telling the truth by Bob that Cathy is stated the truth, makes him in his own a speculator of guilt, the seeming doubt aroused is dismissed by the fact that if the whole house of cards falls down then the first to fall should be the statements of judge not letting the guilty escape without getting the case closed even if mathematically this problem tends to make Bob guilty-really what judge knowing who is guilty at the end with the guilty person stated truth statement, lets this person hang on wheels to iterate another suspect telling something like Cathy did that would be irrelevant totally to the case if it has been Bob?!
Remember Bob or Cathy are equally suspect so it would seem like the judge hears Cathy to get her straight to Alice, because that is the fair shot guilty person all waited for. Alice has one essence to her telling the truth and if it was false then again reinforcing above plus then Cathy herself may be guilty but then she gets the case that Bob is lying and Alice tells something that might be putting her in jeopardy. And again this safe is to the judge that knows who is guilty but due that we are to solve this gets more complicated just because the statement are supposed to be true under oath not in true conscious by the problem and this is a problem in itself for the solving correctly.
In conclusion Cathy said who is guilty and that is the truth cause the judge is saying she knows who is guilty and we will know it by the count of whole true answers. If Cathy states who is innocent that is something else but she states who is guilty then only Alice can be this one, with guilt, since in the conditions the guilty speaks truly, then Bob also is innocent and Cathy says about a fact that is needed in the problem which is who is guilty, adding to the judges knowledge of this fact. Even if Cathy were to lie for us in doubt still she could be incriminating herself we would have Bob telling the truth and Alice and Cathy both guilty, which we have only one guilty in the starting conditions. So Cathy does not sell herself out anyway in this problem. If Bob was the one that Cathy speaks with guilt on then, it would be the case then a circle for the judge could go on like this; Alice is lying in her statement. Bob is telling the truth from scratch everything, even Cathy will need to be evaluated still like herself or Bob guilty and this remaining to be true or false, but in this case remains completely unhinged the problem between Bob or Cathy just the judge knows. So we would be looking for two guilty people not one. And finally if Bob lies also then Cathy remains to incriminate herself as in the judge only case where she could be guilty and lying. Following the justice hints that she knows who is guilty, second the guilty has stated the truth and we should conclude by deducing and not breaking into the case cause again she already knows who is guilty so Alice first off for us is stating the truth as under oath within the system of justice, then even Bob states something infer to Cathy but this just adds the puzzle and the judge is positioning no comment since she knows the truth, since that then she makes the statement that the person with guilt is speaking truthfully for Bob to enter the case of doubt in the mind puzzle; finally with doubt evaluating what Cathy might be saying we get that if Cathy lies Bob is stating a contradiction that fits Cathy Guilty.(she could lie--even by saying someone of the three may be herself is guilty) So this incriminates Cathy. But hypothetically Bob is not out yet. But to incriminate Bob would mean that Cathy is both guilty and innocent in judge's mind when she know exactly who is guilty, since if Bob and Cathy were both lying then even Alice remains to have lied, this makes one contradiction, or all are lying and Bob is just the living criminal.
At this last circle the problem has exhausted the possible cases and truth of solve and in the truth of thanking me for writing the comment I hope the judge is also right.
Not sure if this is an entirely correct solution, but I'll just sketch my thought process.
So, there can be either 1 , 2 , or 3 truthful statements. There cannot be 0 , because then, according to the judge's second statement, no one would be guilty, which is clearly a contradiction. Now, suppose all 3 statements are true. That would mean that we could say Alice is guilty. That is because the first two statements are true, and that leaves only Alice open. However, we can't have this, because the judge told us that knowing the number of true statements and Cathy's words alone were not enough to identify the guilty party. So, we must have either 1 or 2 truthful statements to preserve some sort of ambiguity.
The judge's second statement lets us know that once we know the number of statements as well as the fact that the guilty party gave a true statement, we will know immediately (assuming we are perfect at logical thinking) who the guilty party is. This would be nifty if there was only 1 true statement, because it would mean that with truth comes guilt. So, let's try it out! Say Alice is the only one telling the truth. That implies Alice is guilty. However, we run into a contradiction because Bob must say that Cathy is guilty, but only one person, Alice, is guilty. So that's out. What if Bob was the only one telling the truth, and, consequently, was the guilty party? Well, this works out. Cathy is innocent from Bob's true statement and Alice is innocent because she's not Bob. So, now if we run into a contradiction by checking the last case, we'll know that Bob did it, in the case that there was only 1 true statement.
So, on to the last case: Cathy is telling the truth, and is the guilty party. That means Alice is lying about Bob being innocent, which is a contradiction, since we can only have one guilty party. Therefore, if the judge told us that there was 1 true statement, and the guilty party didn't commit purjury, we would know instantly that Bob was the guilty party. And that's how I arrived at my answer. I didn't want to go into the case of 2 correct statements because I figured this was sufficient, and I'm kind of tired. Fun problem, nonetheless!