Partially Inscribed Triangle
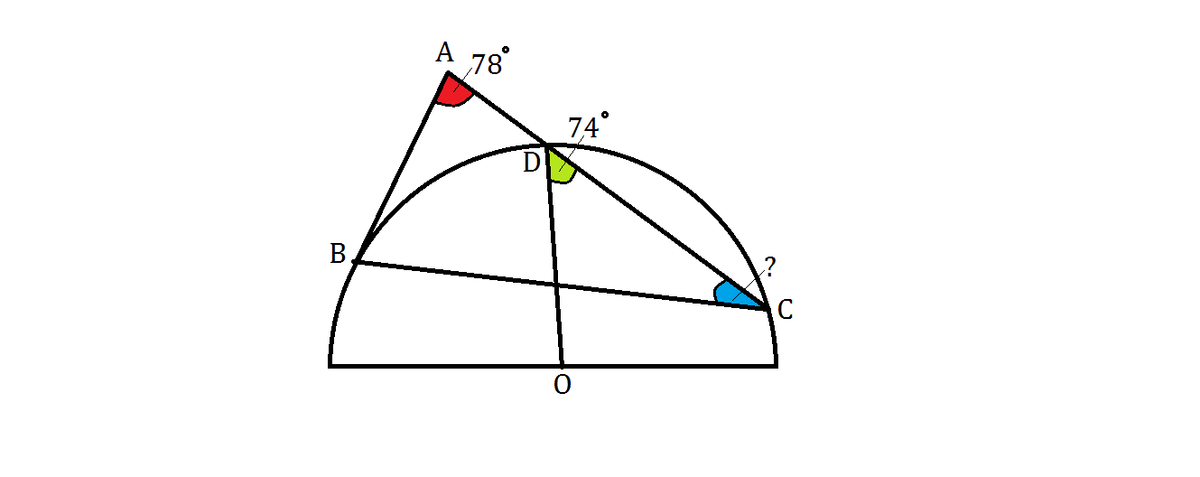
Triangle A B C has vertices B and C on a semicircle centered at O , as shown, with A B tangent to the semicircle at B and A C intersecting the semicircle at point D .
If ∠ B A C = 7 8 ∘ (in red) and ∠ O D C = 7 4 ∘ (in green), what is the measure of ∠ B C A (in blue) in degrees?
Note: The figure is not drawn to scale.
The answer is 43.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
How did you get 2x?
angle subtended at the center is 2x. see as whole circle
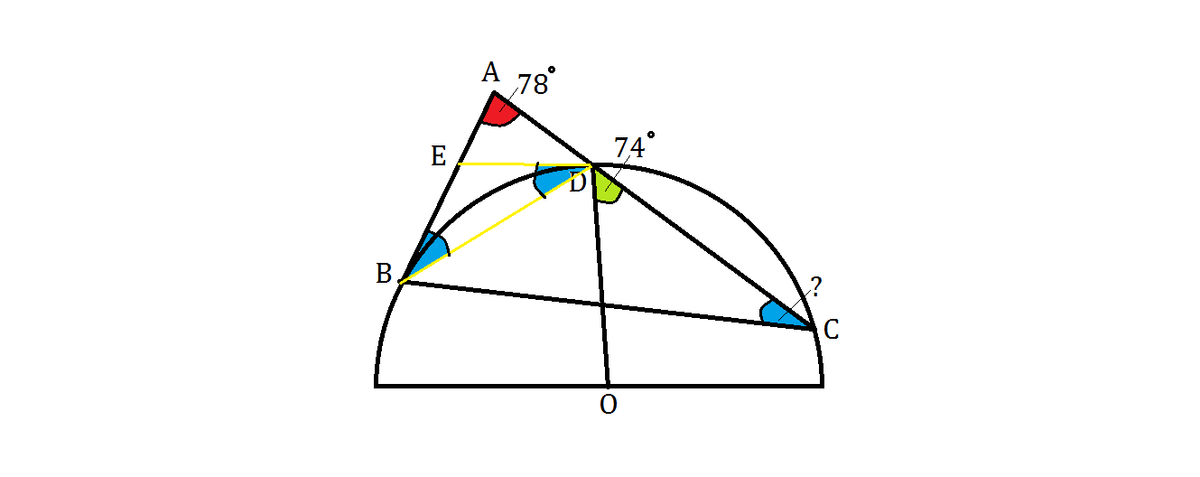
We will begin by drawing the chord B C and another tangent from D to meet the original tangent A B at point E .
According to the Alternate Segment Theorem , ∠ A B D = ∠ B C A = x , as shown in blue.
Also, by Alternate Segment Theorem , ∠ E D B = ∠ B C A = x , regarding E D as the tangent.
Alternatively, since the lengths of tangents of external point are equal, B E = E D , making B E D an isosceles triangle, and so ∠ E D B = ∠ B C A = x .
Then because the radius O D is perpendicular to D E , ∠ B D O = 9 0 ∘ − x .
We can then summarize the equation:
∠ B A D + ∠ A B D = ∠ B D O + ∠ O D C
7 8 + x = ( 9 0 − x ) + 7 4
2 x = 9 0 + 7 4 − 7 8 = 8 6
Thus, x = 4 3 ∘ .
Construct a radius B O then it says ∠ B O D = 2 ∠ B C D , here denotes as ∠ B C D = x , ∠ B O D = 2 x .
Then easily found that ∠ A D O = 1 0 6 ∘ , and ∠ A B O = 9 0 ∘ , then using the sum of internal angle of quadrilateral gives us 9 0 ∘ + 7 8 ∘ + 1 0 6 ∘ + 2 x = 3 6 0 ∘ ⟶ x = 4 3 ∘ .