Solve it anyway!
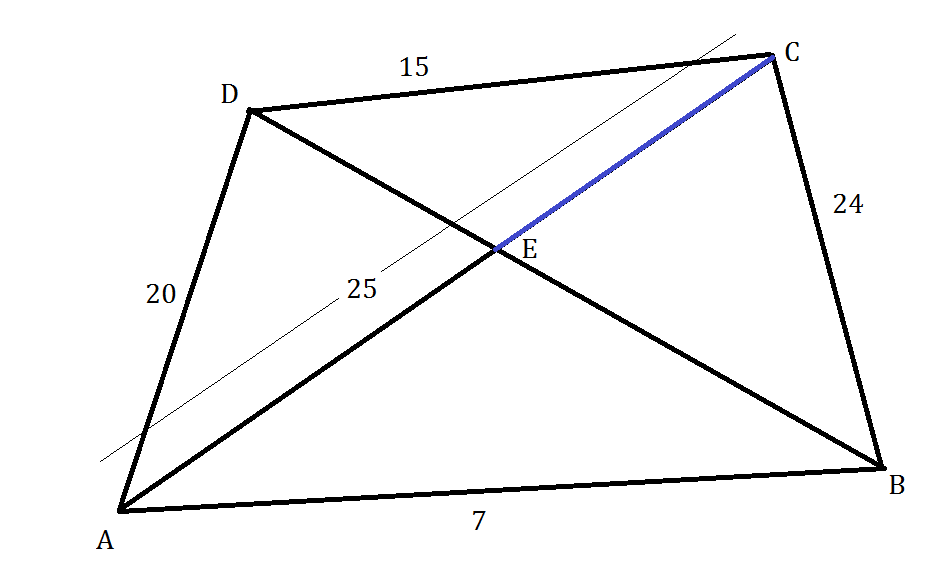In the above given figure determine the length of the blue line EC
The figure is not drawn to scale . Can you solve this without using coordinates?
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Once you observe the cyclic quadrilateral, you can apply the formula
C E A E = C D A B × C B A D .
Do you see why that is true? You alluded to it in your approach, but I think it's obscured in all of the calculations that you did after that.
Log in to reply
Oh ...I agree
I used the technique by using the properties of similar triangles in triangle AED and BEC but didn't use it in the other pair of triangles that is AEB and triangle DEC . to get the formula given by you . That was my mistake although now I have rectified that thanks .
It will be better if you delete yourcomment from my question
I too can but I willn't
good solution i did it the same way
Once you observe the cyclic quadrilateral, a better formula to apply is
C E A E = C D A B × C B A D .
This avoids relying on the condition that the angles are right. It follows from the area observation applied to other triangles.