Partition of a Polygon
There is a
-sided polygon
with the side length as
and
is taken as
. Find all possible partition (through the vertex) of the polygon into two parts such that the difference of the sum of lengths of sides in the two parts is minimum. For clarification of question one partition for
and one for
is shown below. In fact only one partition exists for
and
.
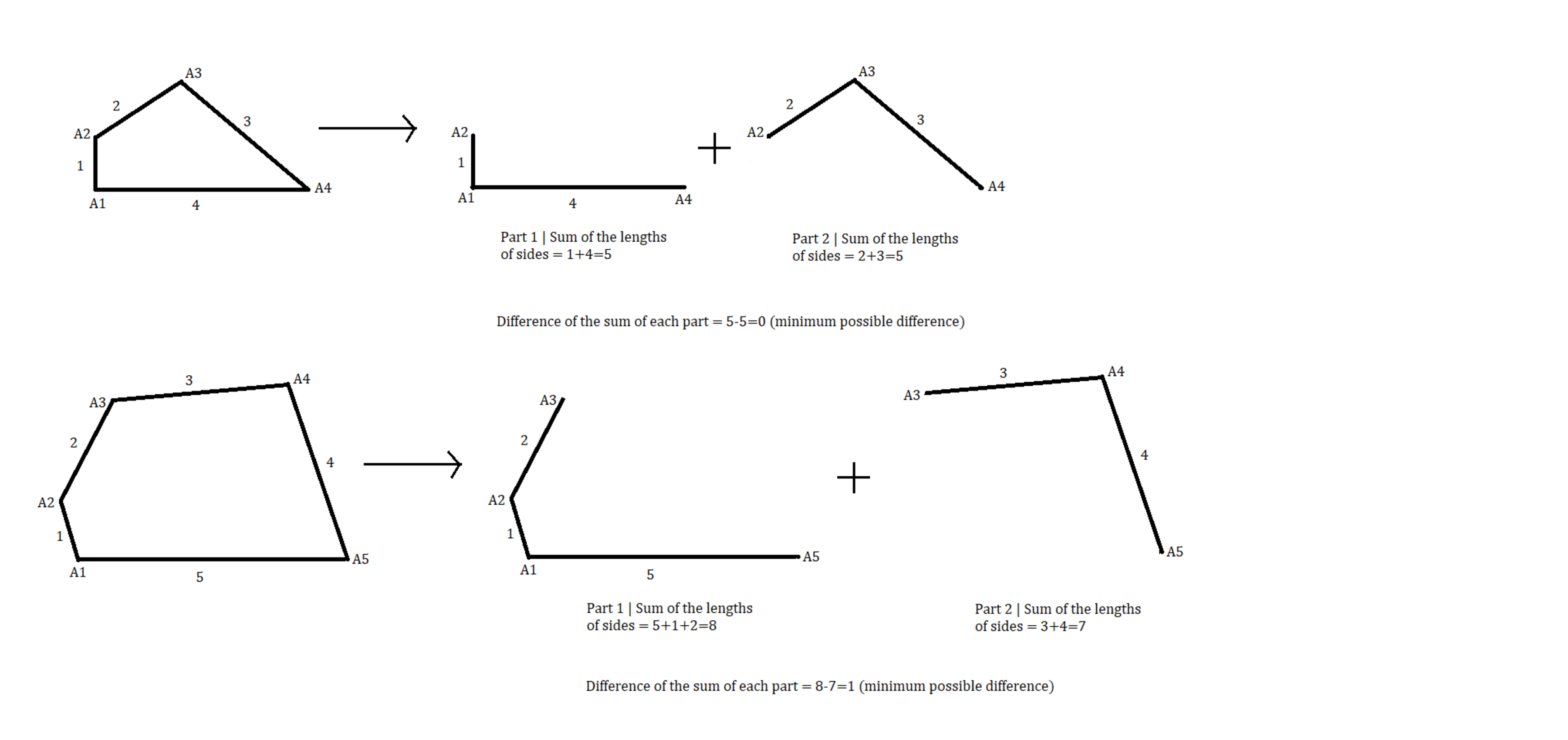 Let
and
be the number of possible partitions for
and
respectively. Find
Let
and
be the number of possible partitions for
and
respectively. Find
BONUS : Solve for possible partitions for any .
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
0 solutions
No explanations have been posted yet. Check back later!