Partitioning Many Triangles
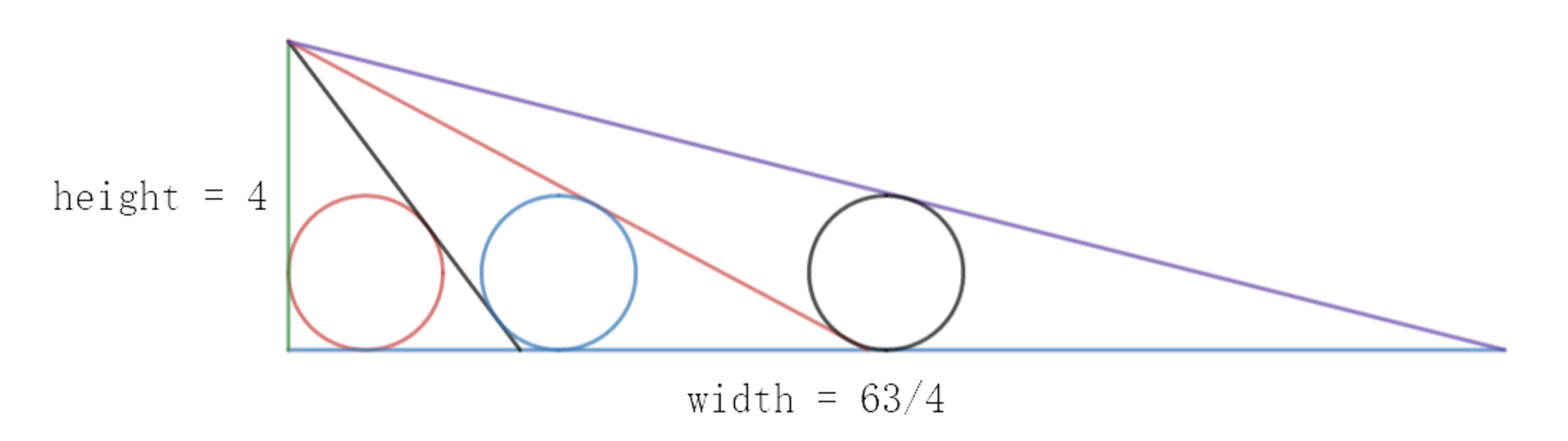
As shown above, a right triangle of height 4 is partitioned into 3 triangles, only one of which is a right triangle. A unit circle is inscribed inside each triangle, and the width of the original right triangle can be found to be 4 6 3 .
Using the same construction, a larger right triangle of height 4 is partitioned into N triangles (only one is a right triangle). Also, a unit circle is inscribed inside each of these triangles. The width of this larger right triangle exceeds 1 0 4 . What is the minimum value of N ?
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Yuppers, this is the exact formula that I got. Can you elaborate on it?
Compare @Hosam Hajjir 's solution for a proof by induction.
Bonus fact: the base of the n th triangle plus the x -coordinate of its incentre is 2 n + 1 .
Log in to reply
Wow! That looks like another extraordinary result :)
Define the width x N is a sequence. We note that x 1 = 3 , x 2 = 2 1 5 , x 3 = 4 6 3 , ⋯ . It would appear that x N = 2 N − 1 4 N − 1 . We can prove this claim using proof by induction as follows:
The area of the last partitioned triangle, Δ N = s r , where s is the semiperimeter of the triangle and r is the radius of the incircle, which is 1 . But Δ N = 2 4 ( x N − x N − 1 ) . Therefore,
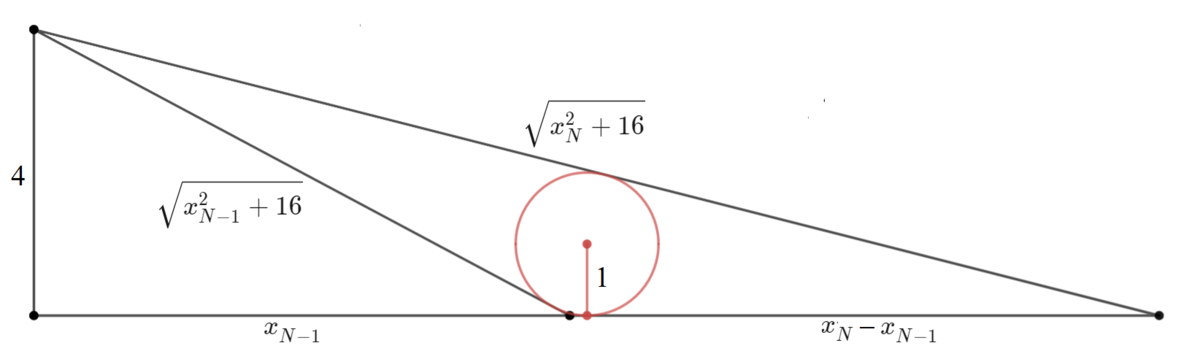
2 ( x N − x N − 1 ) 3 ( x N − x N − 1 ) 3 x N − ( 3 x N − 1 + x N − 1 + 1 6 ) 3 x N − a N − 1 8 x N − 6 a N − 1 x N + a N − 1 2 − 1 6 ⟹ x N = s r = 2 ( x N − x N − 1 ) + x N 2 + 4 2 + x N − 1 2 + 4 2 = x N 2 + 1 6 + x N − 1 2 + 1 6 = x N 2 + 1 6 Let a N − 1 = 3 x N − 1 + x N − 1 + 1 6 = x N 2 + 1 6 Squaring both sides = 0 = 8 3 a N − 1 + a N − 1 2 + 1 2 8
Assuming that the claim x N = 2 N − 1 4 N − 1 is true for N , then
a N a N 2 + 1 2 8 = 3 x N + x N 2 + 1 6 = 2 N − 1 3 ( 4 N − 1 ) + ( 2 N − 1 4 N − 1 ) 2 + 1 6 = 2 N − 1 3 ( 4 N − 1 ) + 2 N − 1 4 N + 1 = 2 N − 2 2 2 N + 1 − 1 = 2 N − 2 2 2 N + 1 + 1
And
x N + 1 = 8 3 a N + a N 2 + 1 2 8 = 2 N + 1 2 2 N + 3 − 2 = 2 N 4 N + 1 − 1
Therefore the claim is also true for N + 1 , and it is true for all N ≥ 1 .
Now we need to find the smallest N such that x N = 2 N − 1 4 N − 1 > 1 0 4 , approximately 2 N + 1 > 1 0 4 ⟹ N = ⌈ lo g 1 0 2 4 − 1 ⌉ = 1 3 .
Starting with the first triangle on the left, its base extends from the origin to ( x ( 1 ) , 0 ) , where x ( 1 ) = 3 , and its hypotenuse is h ( 1 ) = 5 . Now consider the n -th triangle, we want to build the ( n + 1 ) -th triangle on its hypotenuse h ( n ) , so we have to extend the base line to x ( n + 1 ) = x ( n ) + d and we therefore have h ( n + 1 ) = 1 6 + x ( n + 1 ) 2
Since a unit circle is inscribed in this ( n + 1 ) − t h triangle, then 2 A = P , and therefore,
4 d = d + h ( n ) + 1 6 + ( x ( n ) + d ) 2
Simplifying as follows:
3 d − h ( n ) = 1 6 + x ( n ) 2 + 2 x ( n ) d + d 2
Squaring, and noting that 1 6 + x ( n ) 2 = h ( n ) 2 , we obtain,
9 d 2 − 6 d h ( n ) = 2 x ( n ) d + d 2
From which it is straightforward to calculate that
d = 4 3 h ( n ) + x ( n )
Since we have d , then we now have x ( n + 1 ) = x ( n ) + d and h ( n + 1 ) = 1 6 + x ( n + 1 ) 2
Now, all we have to do is write a tiny code to implement a loop in the index n and compute successive values of x ( n + 1 ) , h ( n + 1 ) , starting with x ( 1 ) = 3 , and h ( 1 ) = 5 . We exit the loop when x ( n + 1 ) > 1 0 4 . The number of triangles is N = n + 1 .
Running this code I found that n = 1 2 , and therefore, N = 1 3
The other solution gives a closed form - not that I'm trying to goad you into an induction-off... ;-)
Claim: If the larger right triangle is partitioned into N triangles, then the width (say w ) of the larger right triangle is given by, w = 2 N − 1 2 2 N − 1 Proof: Define w ( k ) to be the width of the larger right triangle with k partitions. Now consider a larger right triangle with N + 1 partitions that has a base length equal to w ( N + 1 ) . Notice that it comprises of a large right triangle with N partitions with base length w ( N ) and 1 smaller triangle (right most triangle) with base length as w ( N + 1 ) − w ( N ) .
Therefore, this smaller triangle has sides 1 6 + w ( N ) 2 , 1 6 + w ( N + 1 ) 2 and w ( N + 1 ) − w ( N ) . Since the inradius of this triangle is 1 , 2 ( w ( N + 1 ) − w ( N ) ) ⟹ 3 ( w ( N + 1 ) − w ( N ) ) = 2 1 6 + w ( N ) 2 + 1 6 + w ( N + 1 ) 2 + w ( N + 1 ) − w ( N ) = 1 6 + w ( N + 1 ) 2 + 1 6 + w ( N ) 2 Solving this as a quadratic in terms of w ( N + 1 ) , we get the relation w ( N + 1 ) = 4 3 1 6 + w ( N ) 2 + 5 w ( N ) Since w ( 1 ) = 3 , it is easy to see that the first few values of the sequence are w ( 1 ) w ( 2 ) w ( 3 ) w ( 4 ) w ( 5 ) = 1 3 = 2 0 2 2 − 1 = 2 9 = 2 1 2 4 − 1 = 4 6 3 = 2 2 2 6 − 1 = 8 2 5 5 = 2 3 2 8 − 1 = 1 6 1 0 2 3 = 2 4 2 1 0 − 1 By induction, we prove that the solution of the above recurrence relation is w ( N ) = 2 N − 1 2 2 N − 1 Hence, our initial claim was correct.
Finally, all we need to do is solve the inequality, 2 N − 1 2 2 N − 1 > 1 0 4 x 4 x 2 − 1 > 1 0 4 , x = 2 N − 1 ⟹ x = 2 N − 1 > 2 5 0 0 ⟹ N ≥ 1 3 Therefore, the minimum value of N that satisfies the above condition is 1 3