Partitions with no 1s

Probability Level 2

$\begin{aligned} p(17) &= 297 \\ p(18) &= 385 \\ p(19) &= 490 \\ p(20) &= 627 \\ p(21) &= 792 \end{aligned}$

Let $p(n)$ be the number of partitions of an integer $n$ . The values of $p(17), p(18),p(19),p(20), p(21)$ are as shown above.

How many partitions of 20 are there that do not contain any parts equal to 1?

The answer is 137.

4 solutions

Jon Haussmann
Feb 19, 2016

For a positive integer $n$ , consider a partition of $n$ that contains a 1. If we remove this 1, then we obtain a partition of $n - 1$ . Conversely, if we take a partition of $n - 1$ and add a 1, then we create a partition of $n$ that contains a 1. Thus, there is a bijection between partitions of $n$ that contain a 1 and partitions of $n - 1$ .

Hence, the number of partitions of 20 that do not contain a 1 is $p(20) - p(19) = 137$ .

It is hard to construct interesting problems about partitions that lend themselves to the Brilliant format (i.e. the answer is a nontrivial number). If you can think of any, it would be much appreciated.

Patrick Corn - 5 years, 3 months ago

I just love your solution, Jon !! For those who would like to see a printout of each partition of 20 which does not have a 1 in it, just execute this bit of code in SAGE :

PL=Partitions(20).list()

cnt=0

for n in srange(0,627):

  if 1 not in PL[n]:

  print PL[n]

  cnt+=1

print cnt

That last print command gives the answer $\boxed{\boxed{137}}$

Bob Kadylo - 5 years, 3 months ago

A Former Brilliant Member
Apr 7, 2019

$\text{Length}[\text{IntegerPartitions}[20,10,\text{Range}[2,20]]] \Rightarrow 137$

I could use Fermat's excuse for not writing out his proof: "The margin is not large enough.," as a reason for not presenting the solution list; but, I will give it anyway in hopes of helping someone .

{{20},{18,2},{17,3},{16,4},{16,2,2},{15,5},{15,3,2},{14,6},{14,4,2},{14,3,3},{14,2,2,2},{13,7},{13,5,2},{13,4,3},{13,3,2,2},{12,8},{12,6,2},{12,5,3},{12,4,4},{12,4,2,2},{12,3,3,2},{12,2,2,2,2},{11,9},{11,7,2},{11,6,3},{11,5,4},{11,5,2,2},{11,4,3,2},{11,3,3,3},{11,3,2,2,2},{10,10},{10,8,2},{10,7,3},{10,6,4},{10,6,2,2},{10,5,5},{10,5,3,2},{10,4,4,2},{10,4,3,3},{10,4,2,2,2},{10,3,3,2,2},{10,2,2,2,2,2},{9,9,2},{9,8,3},{9,7,4},{9,7,2,2},{9,6,5},{9,6,3,2},{9,5,4,2},{9,5,3,3},{9,5,2,2,2},{9,4,4,3},{9,4,3,2,2},{9,3,3,3,2},{9,3,2,2,2,2},{8,8,4},{8,8,2,2},{8,7,5},{8,7,3,2},{8,6,6},{8,6,4,2},{8,6,3,3},{8,6,2,2,2},{8,5,5,2},{8,5,4,3},{8,5,3,2,2},{8,4,4,4},{8,4,4,2,2},{8,4,3,3,2},{8,4,2,2,2,2},{8,3,3,3,3},{8,3,3,2,2,2},{8,2,2,2,2,2,2},{7,7,6},{7,7,4,2},{7,7,3,3},{7,7,2,2,2},{7,6,5,2},{7,6,4,3},{7,6,3,2,2},{7,5,5,3},{7,5,4,4},{7,5,4,2,2},{7,5,3,3,2},{7,5,2,2,2,2},{7,4,4,3,2},{7,4,3,3,3},{7,4,3,2,2,2},{7,3,3,3,2,2},{7,3,2,2,2,2,2},{6,6,6,2},{6,6,5,3},{6,6,4,4},{6,6,4,2,2},{6,6,3,3,2},{6,6,2,2,2,2},{6,5,5,4},{6,5,5,2,2},{6,5,4,3,2},{6,5,3,3,3},{6,5,3,2,2,2},{6,4,4,4,2},{6,4,4,3,3},{6,4,4,2,2,2},{6,4,3,3,2,2},{6,4,2,2,2,2,2},{6,3,3,3,3,2},{6,3,3,2,2,2,2},{6,2,2,2,2,2,2,2},{5,5,5,5},{5,5,5,3,2},{5,5,4,4,2},{5,5,4,3,3},{5,5,4,2,2,2},{5,5,3,3,2,2},{5,5,2,2,2,2,2},{5,4,4,4,3},{5,4,4,3,2,2},{5,4,3,3,3,2},{5,4,3,2,2,2,2},{5,3,3,3,3,3},{5,3,3,3,2,2,2},{5,3,2,2,2,2,2,2},{4,4,4,4,4},{4,4,4,4,2,2},{4,4,4,3,3,2},{4,4,4,2,2,2,2},{4,4,3,3,3,3},{4,4,3,3,2,2,2},{4,4,2,2,2,2,2,2},{4,3,3,3,3,2,2},{4,3,3,2,2,2,2,2},{4,2,2,2,2,2,2,2,2},{3,3,3,3,3,3,2},{3,3,3,3,2,2,2,2},{3,3,2,2,2,2,2,2,2},{2,2,2,2,2,2,2,2,2,2}}

Hitesh Yadav
Apr 13, 2020

To have partitions of 20 where none of the parts equal 1, we'll have to subtract partitions of 20 having parts containing 1 from total no.of parts. So desired number is p(20)-P(20,1). From our theorem in identical objects into identical bins p(20,1)=p(19).Thus desired number is p(20)-p(19). =>627-490=137.

Ariel Gershon
Feb 19, 2016

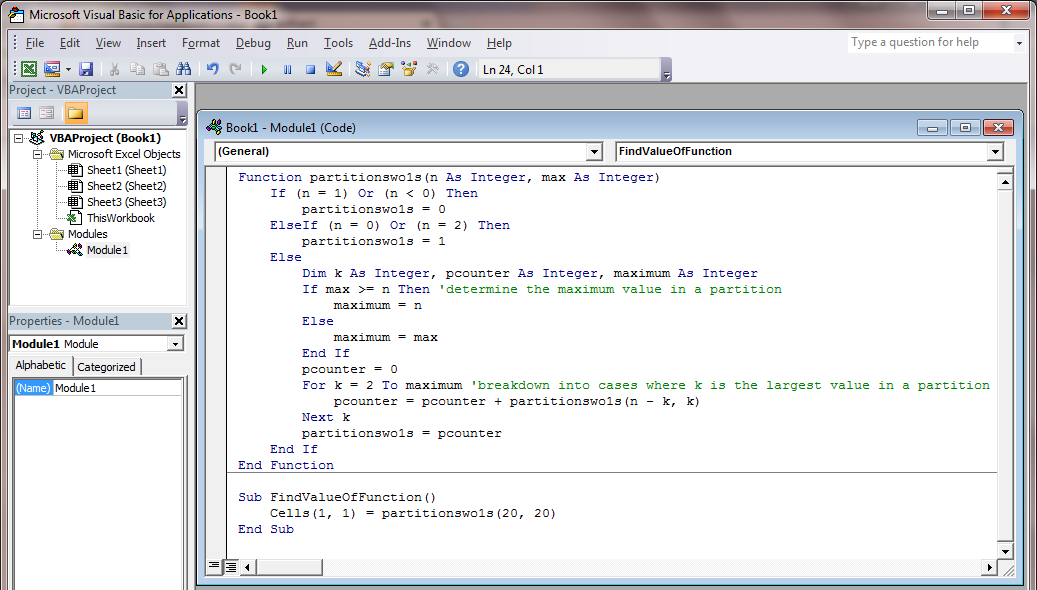
I simply wrote this code in Excel VBA:

Partitions with no 1s

The answer is 137.

4 solutions

0 pending reports