Party
The map below represents a neighborhood. Each node represents a house, and the segments represent the paths between those houses. Alice's house is shown in red, and Bob's house is shown in green.
Alice is going to Bob's house to celebrate his birthday. For each house that she visits along the way, she will invite one person from that house. Additionally, Alice will not visit the same house (including her own house) or pass through the same path more than once.
What is the maximum even number of people Alice can invite?
Details and Assumptions:
- Alice cannot turn while in the middle of a path represented by a black line segment, she can only turn while at one of the houses.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The directions don't say that she has to take a "straight" path from one house to the next ... therefore if she travels half way up a path and then turns on an angle towards another house, not in a straight line path, she can visit all 8 without walking on the same part of any path twice, before going to Bob's. answer 8
Log in to reply
I agree, at best this is a poorly worded problem.
The answer is clearly 8 if Alice simply makes a few turns when the paths cross. There is nothing in the problem that would suggest that cannot be done.
If that was part of the conditions for the problem it should be stated in the problem. Even with that unstated condition, the correct answer is still not 6 but 7. If we number the houses counterclockwise around the larger outer group as Alice's house number one the first to the left as number 2 and so on so that the outer group in numbered 1 to 5.The inner group, bobs house number 10 the first to the left as number 6.
Alice's path would be 1,2,3,4,5,9,6,8,10 that is seven houses other then Allies' or Bobs house
The point is either the path crosses itself between the various houses making it possible to turn and simply go to the next house in a sequence around the group (8 people) or somehow the path does not cross itself it that case we do not have to worry about going thru the same path twice(7 people).
You are quite right, obviously, as anyone can see within two seconds with an unconditioned mind.
The problem maker should write that changing directions is not allowed,otherwise clearly ans is 8
Log in to reply
By changing directions we can have 8 guests. Either we can have 8 guests or 0 guests because if we see the changing directions of the sides of Pentagon then we can't have a single guest.
This is incorrect
Even without using one of the pedantic suggestions below, the answer is 7. The solution shown is patently wrong. If one follows the outside path CCW, then enters the right home, crosses left, then lower right before arriving at Bob's how she will not have reused any path or house. 7.
Log in to reply
I also count 7 without using twice the same path, just as you described. Outside path then inner star
I'm also counting 7. Am I wrong or is the problem wrong? EDIT: I now notice the insertion of "even" into the final problem question. Now with the added assertion that there is no turning....seems a bit of a poorly thought out problem
Log in to reply
"Even number" has always been there. What we did was bold the term (first just "even", then "even number"), because the discussion showed that most people missed it.
If she heads to left, bottom left, bottom right, up to left, up to left, right, down left and Bob's house, 7 houses. Sorry for the comment, I write it wrong.
I think you're wrong. 0 Alicia/ 1 x Bob 4 8 5 7 6 2 3 1-2-3-6-8-5-7-X 7 houses
Counting Alice and Bob's houses, I think she can visit 8.
Log in to reply
Alice's and Bob's houses shouldn't be counted. Note that the problem asks how many people can Alice invite. She can't invite herself and Bob, can she?
I got exactly that answer too!
- If the dots were numbered I could show you the sequence. Top down left. Then in to outer star (top left). Then bottom left star. Then bottom left of pentagon. Go right to bottom right. Go up to top right of pentagon. Come in to top right star. Then down to bottom right of star. Go up to left cross over one line. At intersection of next line turn up and right. 8. No path travelled twice.
Why can't Alice visit every blue house, though? The question doesn't say anything against it.
Log in to reply
How can Alice visit every blue house without visiting the same house more than once, and then arrive at Bob's?
Log in to reply
I'm sorry, I thought she could. I looked over the problem and found it was impossible.
If she comes back to her own house before she goes to Bob's house then she can visit all 8 houses. Go left then diagonal, across bottom, other diagonal then back to red house before blue house.
If we can change direction along a path then we can visit all 8 easily Eg numbering blue houses left to right for 3 rows: 1st row 1,2,3,4 2nd row 5,6 3rd row 7,8. Move in sequence 1, 2 3, 4,8,7,5 then changing direction at the intersection to 6 then to green. dDe. Seems the assumption is we can't change direction at an intersection which is not logical
I got 8 because she invited one guest from her own house, and one guest from Bobs.
I got 8. It does not say that you have to start at Alice's house. You can start at the house to the south west of Alice's house, go diagonally south east, then west, then diagonally north east, then to Alice's house, then to Bob's house. No turns, all blue houses visited only once, and paths only used once.
awfully put together, this one... the little "even" number caveat, jeez... might as well word it as "what is the highest number that starts with the letter S"
Alice can visit 7 houses before arriving to Bob's house. 7 should be the right answer.
Log in to reply
Can you explain why it is 7? Note that the problem stated what is the maximum even number of people Alice can invite.
7————————7
The answer is 6. But max is 7
We can invite 6 guests as follows: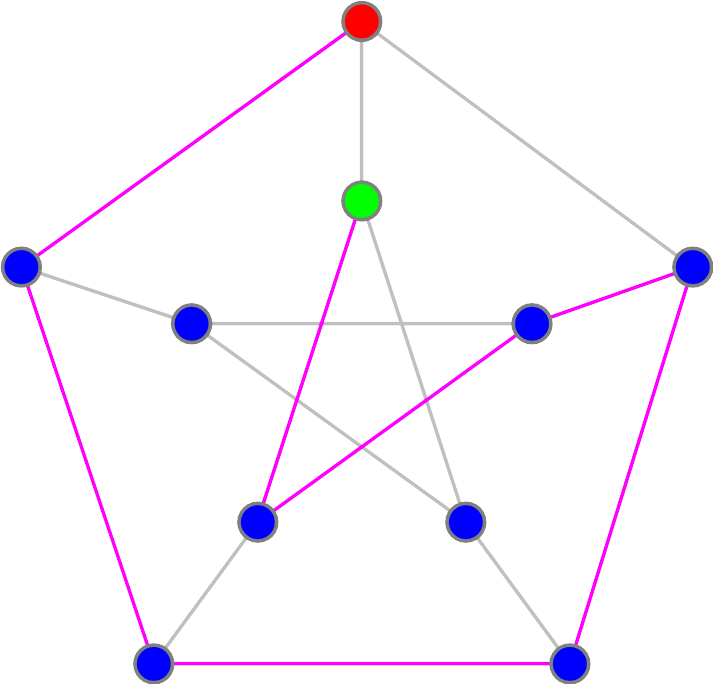 So we need to show that we can't invite 8 guests. This would mean visiting every blue house exactly once along the way.
So we need to show that we can't invite 8 guests. This would mean visiting every blue house exactly once along the way.
Of course, we can ignore the path that goes directly from Alice's to Bob's house. Without loss of generality, assume that Alice first heads to our left. Furthermore, Alice's route can go through the house on the far right in only one way: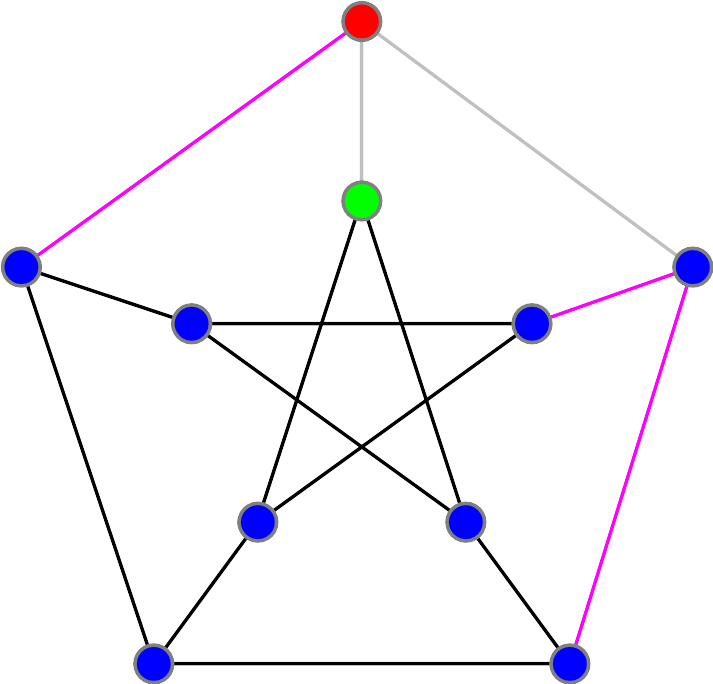 Now, there are two paths leading to Bob's house. Suppose the one coming from the left is used, and try to form a path step by step:
Now, there are two paths leading to Bob's house. Suppose the one coming from the left is used, and try to form a path step by step:
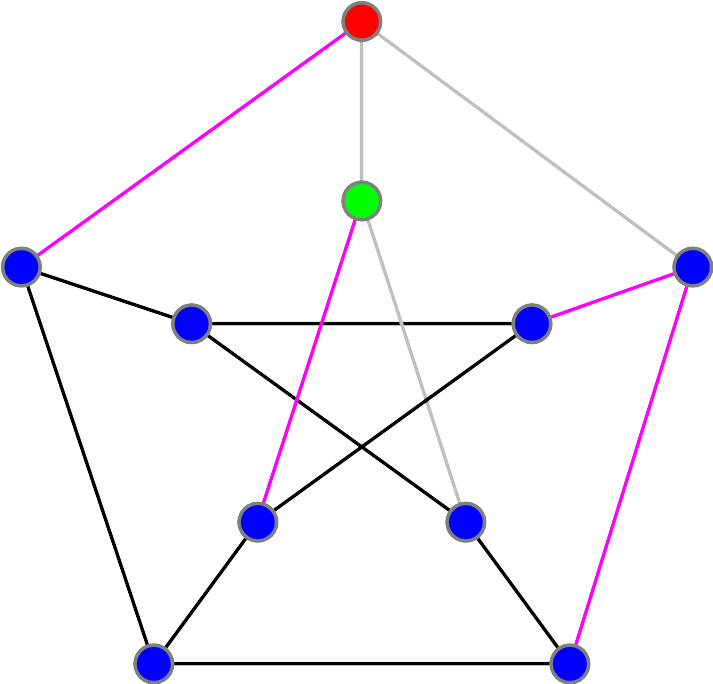
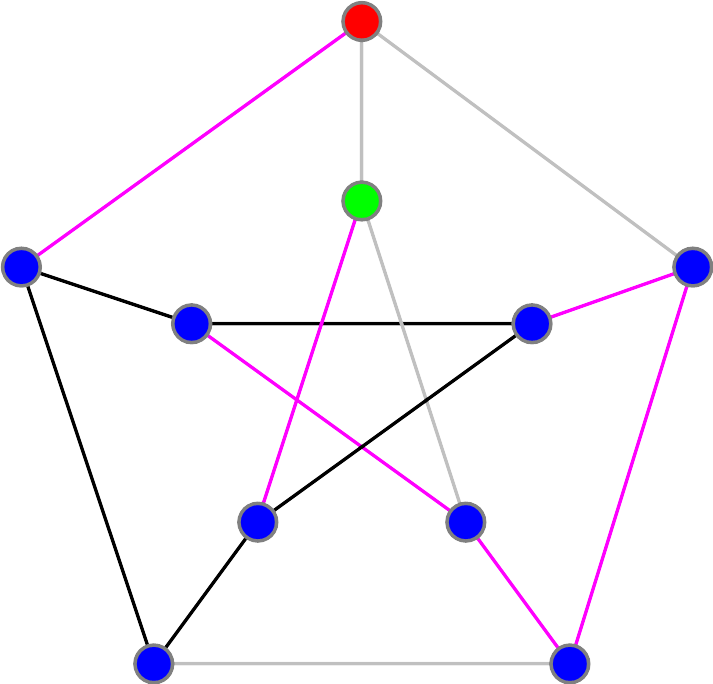
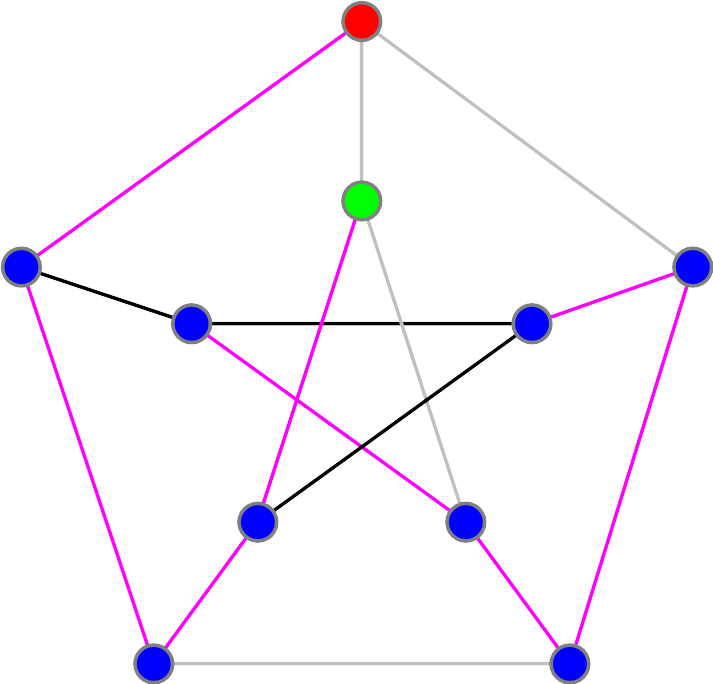 As you see, as we fill in or eliminate the paths we are forced to, we get stuck. The same happens if we reach Bob's house via the path coming from the right.
As you see, as we fill in or eliminate the paths we are forced to, we get stuck. The same happens if we reach Bob's house via the path coming from the right.
As such, 8 is impossible, and so 6 is the maximum even number possible.