Pascal and Current Year
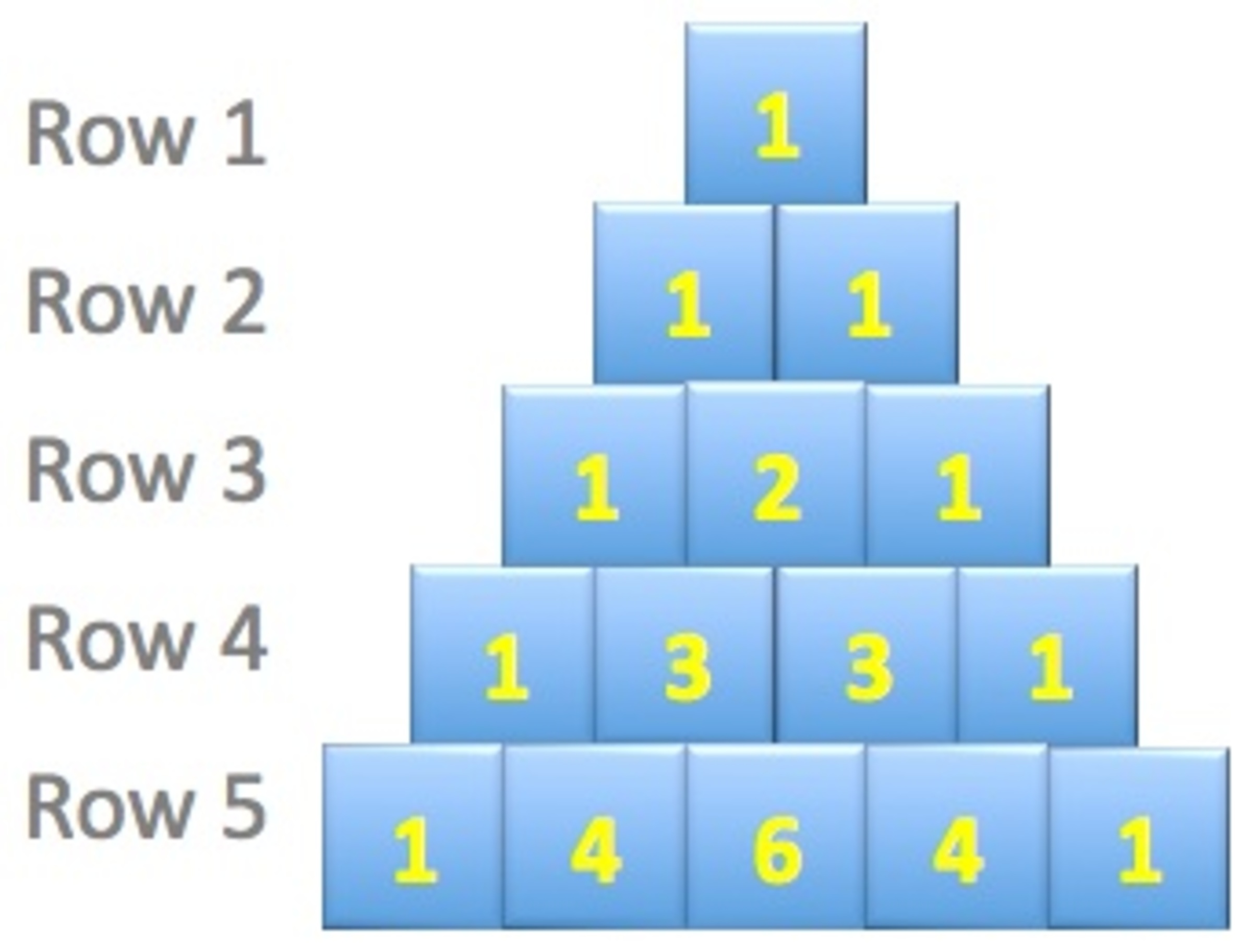 The given picture represents the Pascal triangle. What is the sum of the numbers in the 2018th row?
The given picture represents the Pascal triangle. What is the sum of the numbers in the 2018th row?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Sir, something went wrong with your LaTeX.
Thank you, nice solution.
Note that:
Row 1: sum of numbers is 2 1 − 1 = 2 0 = 1
Row 2: sum of numbers is 2 2 − 1 = 2 1 = 2
Row 3: sum of numbers is 2 3 − 1 = 2 2 = 4
Row 4: sum of numbers is 2 4 − 1 = 2 3 = 8
Thus, sum of numbers in the Row 2018 is : 2 2 0 1 8 − 1 = 2 2 0 1 7
Relevant wiki: Binomial Theorem
By binomial theorem, we have ( 1 + x ) n = k = 0 ∑ n ( k n ) x k . Putting x = 1 , ⟹ k = 0 ∑ n ( k n ) = 2 n . That is the sum of numbers of the ( n + 1 ) th row of Pascal triangle is equal to 2 n . Therefore, that for the 2018th row is 2 2 0 1 7 .