Pascal Variant
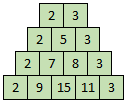
A Pascal-like Triangle, where each entry of each subsequent row is constructed by adding the number above and to the left with the number above and to the right, is started with ( 2 , 3 ) in the 1 st row, so that the 2 nd row is ( 2 , 5 , 3 ) , the 3 rd row is ( 2 , 7 , 8 , 3 ) , the 4 th row is ( 2 , 9 , 1 5 , 1 1 , 3 ) , and so on.
Find the 4 th number in the 1 0 0 0 th row.
The answer is 332832501.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
In any Pascal-like triangle, the k th number in the n th row is the sum of the entries in the ( k − 1 ) th diagonal, up to row n − 1 . For example, the 3rd entry in the fourth row is 1 5 , which is also the sum of the entries in the 2nd diagonal up to row 3 ( 3 + 5 + 7 = 1 5 ).
Note that, since we start with 3 and add 2 every time, the 2 nd diagonal is the odd integers (starting with 3 ). Therefore, the n th entry (by which I mean the entry in row n ) in the 3 rd diagonal is simply the sum of the first n − 1 odd numbers (not counting 1 ). Or, alternatively, the sum of the first n odd numbers minus 1 . But the sum of the first n odd numbers is n 2 . So the n th entry in the third diagonal is n 2 − 1 .
Now, consider the fourth diagonal. The n th entry will be the sum of the previous n − 1 entries in the third diagonal. So we have i = 1 ∑ n − 1 ( i 2 − 1 ) = i = 1 ∑ n − 1 ( i 2 ) − ( n − 1 ) = 6 n ( n − 1 ) ( 2 n − 1 ) − ( n − 1 ) where the final equality comes from evaluating the identity i = 1 ∑ k i 2 = 6 k ( k + 1 ) ( 2 k + 1 ) at k = n − 1 . All that remains is to calculate 6 1 0 0 0 ⋅ 9 9 9 ⋅ 1 9 9 9 − 9 9 9 = 3 3 2 , 8 3 2 , 5 0 1
Very nice solution!
Well,I did it the same way.
This is basically a linear combination of Pascal's triangles, so that the k th element in the n th row is X n , k = 2 ( k n ) + ( k − 1 n − 1 ) 0 ≤ k ≤ n This makes X 1 0 0 0 , 3 = 3 3 2 8 3 2 5 0 1 .
Nice clean solution!
@Mark Hennings Wait........how did you arrive at this result??? I didn't get it Sir.........could you please elaborate it more......
Log in to reply
If you start with 2 , 2 in the top row, then you obtain double the normal Pascal's Triangle (without the top number). That puts 2 ( k n ) in the k th position of the n th row. If you start with 0 , 1 in the top row, you obtain a normal Pascal's Triangle, flanked by a diagonal of 0 s down the LHS. That puts ( k − 1 n − 1 ) in the k th position of the n th row. Now just add these up.
Log in to reply
Ohhhh!!! This is nice!!!! Thanks a lot, Sir....!! It is always great to learn from your solutions!! They are truly nice!!
@Mark Hennings, sir I think there is a typo in X(1000,3). Shouldn't it be 1000,4 ??
Also,sir, by putting (n,k)= (3,3), we don't get 8.
Log in to reply
As in Pascal’s triangle, the index k starts at 0 , so X n , k is in fact the ( k + 1 ) st element in the n th row.
I solved it a little differently. I saw the pattern of the fourth row which is: 3,11,26,50 etc... which has the difference of 8,15,24 etc... which is simply (3^2-1), (4^2-1) and so on. So I know that by this logic, the 1000th row would the 998th element of this sequence because the fourth number only appears starting from the third row. Now, by this logic, this element would be equal to: 3+(3^2-1)+(4^2-1)...+(999^2-1) which is equal to all the sum of perfect squares from 1 to 999 (which is a simple formula) minus the sum of 1^2 and 2^2, minus 997 (due to the -1's in the sum) plus the 3 in the equation. That gives the solution!
Breaking down the 2 's and 3 's in each entry, we obtain the following:
where the number of 2 's and 3 's follow the pattern of two Pascal Triangles, one for the 2 's on the left side, and one for the 3 's on the right side:
Using the equations for Pascal's Triangle, the m th number in the n th row has ( m − 1 n − 1 ) 2 's and ( m − 2 n − 1 ) 3 's, making the entry equal to 2 ( m − 1 n − 1 ) + 3 ( m − 2 n − 1 ) .
Therefore, the 4 th number in the 1 0 0 0 th row is 2 ( 4 − 1 1 0 0 0 − 1 ) + 3 ( 4 − 2 1 0 0 0 − 1 ) = 3 3 2 8 3 2 5 0 1 .