Pascal's Kissing Circles Triangle
Pascal's Kissing Circles Triangle is constructed in the following manner: in row 0 (the topmost row), there is a unique nonzero entry 1 , then each subsequent row also starts and ends with 1 , but the numbers in between are obtained by finding the radius of the smaller circle that is tangent to a line and two other circles tangent to that line and to each other whose radii are given by the numbers directly above it.
For example, the middle number in row 2 (the third row) that is underneath the 1 and 1 would be the radius of the smaller circle that is tangent to a line and two other circles whose radii are 1 and 1 that are also tangent to that line and to each other.
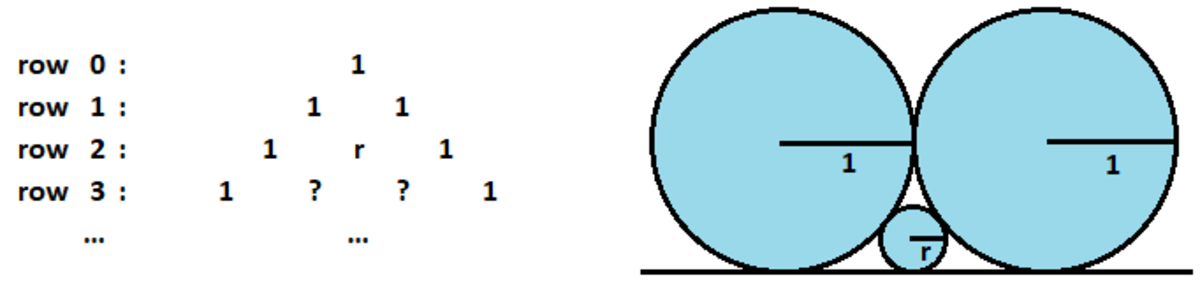
If the middle number of row 1 0 can be expressed as b a , where a and b are relatively prime integers, find a + b .
The answer is 63505.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Nicely done!
Log in to reply
Thanks! Now, how on earth did you find this?! It's a crazy (but very neat) result.
Log in to reply
Thanks! I found it by playing around with Pascal's Triangle. I was thinking that in the regular Pascal's Triangle each number is the sum of the two segments above it if the segments above it are at a 1 8 0 ° angle. So I wondered what would happen if I changed the angle and if I could make a question about it. Changing the angle to 9 0 ° (so that each number is the hypotenuse where the two numbers above it are legs) gives Pascal's Triangle with square roots: ( 1 ) , ( 1 , 1 ) , ( 1 , 2 , 1 ) , ( 1 , 3 , 3 , 1 ) , etc. but that didn't seem challenging enough. Changing the angle to 6 0 ° gives a Pascal's Triangle with all ones which was too easy. Changing the angle to 1 2 0 ° gives a Pascal's Triangle with a lot of nested square roots which was too messy. I thought that 9 0 ° was my best choice, which used a 2 + b 2 = c 2 , but then I remembered that the kissing circles equation had a similar format but with a different exponent ( r 1 − 2 1 + r 2 − 2 1 = r 3 − 2 1 ), and when I tried it it worked out nicely but was also somewhat challenging and so I put it in the form of a question.
Is there any geometric interpretation of this? For example, the number of rectangles in a n × n grid is ( 2 n + 1 ) 2 , which makes sense because you are trying to choose two distinct lines from n + 1 lines - TWICE. It's way more intuitive when you think of it like that. Great solution though :), I also used the kissing circles theorem.
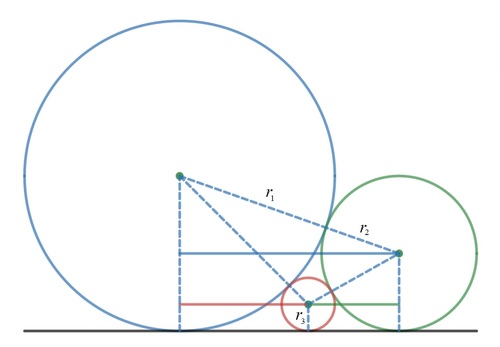
From this problem , it is learned that the relationship of the radii of three circles each tangents to the other two and to the base line as shown above is given by (see proof below):
r 3 1 = r 1 1 + r 2 1 ⟹ r 3 = r 1 + r 2 r 1 r 2
Consider the Pascal's triangle of square root of radius r n k , where n and k are the row and column numbers respectively:
r o w 0 : r o w 1 : r o w 2 : r o w 3 : r o w 4 : 1 1 1 4 1 1 3 1 1 2 1 6 1 1 3 1 1 4 1 1 1
It is obvious from the above that r n k = ( k n ) 1 ⟹ r n k = ( k n ) 2 1 . Therefore r 1 0 , 5 = ( 5 1 0 ) 2 1 = 2 5 2 2 1 = 6 3 5 0 4 1 ⟹ a + b = 6 3 5 0 5 .
Proof: Note that the horizontal distance between the center of the blue circle and the center of the green circle or the length of the full blue line is ℓ b l u e = ( r 1 + r 2 ) 2 − ( r 1 − r 2 ) 2 = 2 r 1 r 2 . Similarly, the lengths of the red line and green line are ℓ r e d = 2 r 3 r 1 and ℓ g r e e n = 2 r 2 r 3 respectively. Now we have:
ℓ b l u e r 1 r 2 r 3 1 = ℓ r e d + ℓ g r e e n = r 3 r 1 + r 2 r 3 = r 2 1 + r 1 1 Divide both sides by r 1 r 2 r 3
You have assumed that the fraction desired simplifies to a fraction whose denominator is at most 1 0 7 . That is not justified.
With the relationship between Ford's circles: 1 / r m i d d l e = 1 / r l e f t + 1 / r r i g h t . We just evaluate the first rows of the triangle, and then, by hard induction we come to the conclusion that every value in the pascal triangle is replaced by the multiplicative inverse of it´s square.
Much like these circles, Pascal apparently came up against Descartes a few times. Happily, they can help each other here; we first need Descartes' circle theorem , which relates the radii of mutually tangent circles, specifically for the case when one of the circles is a straight line. Given two circles of radius a and b , externally tangent to each other and to a straight line, the circle theorem states that the radius c of a third smaller circle tangent to the circles and line is given by c 1 = a 1 + b 1 + a b 2
For example, the " r " in the question can be found by r 1 = 1 1 + 1 1 + 1 × 1 2 = 4 so that r = 4 1 .
Borrowing notation from Pascal's triangle, let R ( n , k ) denote the k th entry of the n th row of the triangle (counting both from zero). We then have R ( n , 0 ) = R ( n , n ) = 1 and R ( n , k ) 1 = R ( n − 1 , k − 1 ) 1 + R ( n − 1 , k ) 1 + R ( n − 1 , k − 1 ) R ( n − 1 , k ) 2 for 0 < k < n .
Computing a few of these, we find the triangle starts as 1 1 1 4 2 1 1 3 2 1 1 2 2 1 6 2 1 1 3 2 1 1 4 2 1 1 1
which Pascal would definitely recognise. This immediately leads to the conjecture that R ( n , k ) 1 = ( k n ) 2
It's easy to see that this works at the ends of the rows, and (as above) for the first few rows. We need to show that R ( n , k ) 1 = R ( n − 1 , k − 1 ) 1 + R ( n − 1 , k ) 1 + R ( n − 1 , k − 1 ) R ( n − 1 , k ) 2 still holds.
Substituting in, the right-hand side is R ( n − 1 , k − 1 ) 1 + R ( n − 1 , k ) 1 + R ( n − 1 , k − 1 ) R ( n − 1 , k ) 2 = ( k − 1 n − 1 ) 2 + ( k n − 1 ) 2 + 2 ( k − 1 n − 1 ) ( k n − 1 ) = ( ( k − 1 n − 1 ) + ( k n − 1 ) ) 2 = ( k n ) 2
which is exactly what we wanted to show.
Finally, to answer the question, R ( 1 0 , 5 ) = ( 5 1 0 ) 2 1 = 2 5 2 2 1 = 6 3 5 0 4 1
so the answer is 6 3 5 0 5 .