Passing through each other's centers
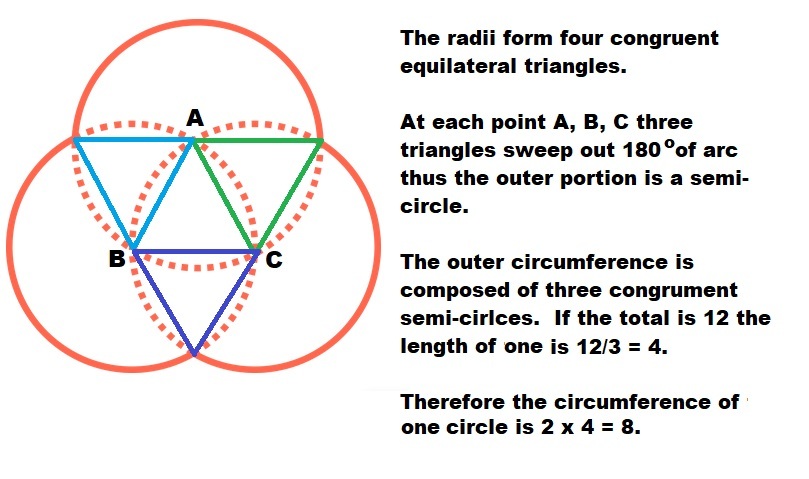
The figure at right consists of 3 identical circles which pass through each others' centers.
If the thicker, outer perimeter has length 12, what is the circumference of one of the 3 identical circles?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
16 solutions
excellently solved.
Perfect, Thank you!
Thanks for the visual
Because all circles pass through each other's centers, the total perimeter consists of 3 half circles, so a half circle is 12/3 = 4. The whole perimeter of 1 circle must be 8.
Moderator note:
Note this proof is incomplete: it doesn't justify why the circle portions are half-circles.
I love the simplicity of this explanation.
That is simple
@challenge master: it was a quick drop of a solution. Proofed the why for myself with equilateral triangles like @Shreyansh Mukhopadhyay did above.
Log in to reply
Yes - and this kind of solution can be valuable - just want to be clear for readers what's going on.
Because when the circles are touching the centres of each one, the portion become the half. This is a generic rule.
I disagree. The reasoning is as conclusive as that of the original problem. Saying that a circle is two semicircles would had been unnecessary. I think
Challenge master was just noting valuable info in reguards to other valuable info
as,all circles pass through each others centers,the total perimeter is actually for 2 1 + 2 1 + 2 1 = 2 3 circles
we know that ,the perimeter of a circle is = 2 τ r
now,
2 τ r × 2 3 = 1 2
or, 2 τ r = 1 2 × 3 2 = 8 square unit. .............[answer]
As the circles pass through each others centres, the intersection of any two circles that is not on the bold line must be the centre of a third circle.
As a result, the bold line is 3 semi-circles, having a perimeter of 12. Therefore the circumference of each circle is (12/3)*3 = 8.
https://sciencevsmagic.net/geo/#0A1.1A0.2A0.3L4
The line here is drawn from the intersection points of the other two circles. That it goes through the center, and is therefore a diameter, gives us a crucial step: each circle is contributing half of its circumference to the circumference of the whole shape. There are three circles. The rest is left as an exercise for the reader.
Nice website! You should promote your website on this site too .
The figure can be drawn with three regular hexagons inscribed within each circle part, the middle most equilateral triangle (1/6 of the regular hexagon) shared between all the triangles, and the three that share an edge with the central most triangle are shared between two of the hexagons.
Remaining, each overlapped circle has their separate 1/2 hexagon (with outer perimeter (ignoring the flat surface that it has been halved across) also half that of the full hexagon). Because these outer half hexagons are inscribed in the circle, and are regular, we notice that the part of the circle (which is included in the perimeter which = 12) starts and ends at what we now know are opposing points of the hexagon, (or vertices of the equilateral triangle we formed by adding three congruent triangles to the centre most one) so is a semi circle.
We can now do:
12/3 (Full perimeter/ Parts of that perimeter) = 4, which is the curved edge of the semi circle (half of the full circle), so 4*2 which =8
Hence 8
The three circles are identical, so you can split the total perimeter of the thick line into three. 1. 12/3 = 4 Then, I assumed that half of one circle’s circumstance is thick and half is thin, so I multiplied my result by 2 to receive my answer. 2. 4x2= 8 8 is the circumstance of one identical circle
Just imagine my sayings
From the given diagram just remove one circle form bottom two, and in mirror see them now you can see that the circles on the thicker side are half circles
My clumsy solution is this: The thicker perimeter consists of 3 halves of the circumference of the circles (c), so 3/2c=12. Therefore the circumference of 1 circle is 12÷3/2=8
Nothing clumsy about that!
For completeness, can you prove that they are 3 halves of a circumference?
Log in to reply
Since the circles are identical and pass through each others centers the outer perimeter must consist of halves of the circumference of the circles. It kind of makes intuitive sense to me, but I haven't learnt the geometry in depth yet, so can't derive a formula for it.
As the shape is symmetrical, the perimeter can be divided into 3 equal semicircles each having perimeter = 4. So circumference of any circle is 2*4=8
because all the circles are passing through each other's centers so that they cut the circumference of each other into half that's why we have the total circumference 1/2+1/2+1/2=3/2 3/2 of circumference is 12 so that 2/3*12=8 is the right answer
3 1/2 circles totaling 12 divided by 3 equals 4 x 2 equals 8
As the perimeter is sum of three semicircles so r comes out to be14/11 then using 2pi r we getthe answer 8
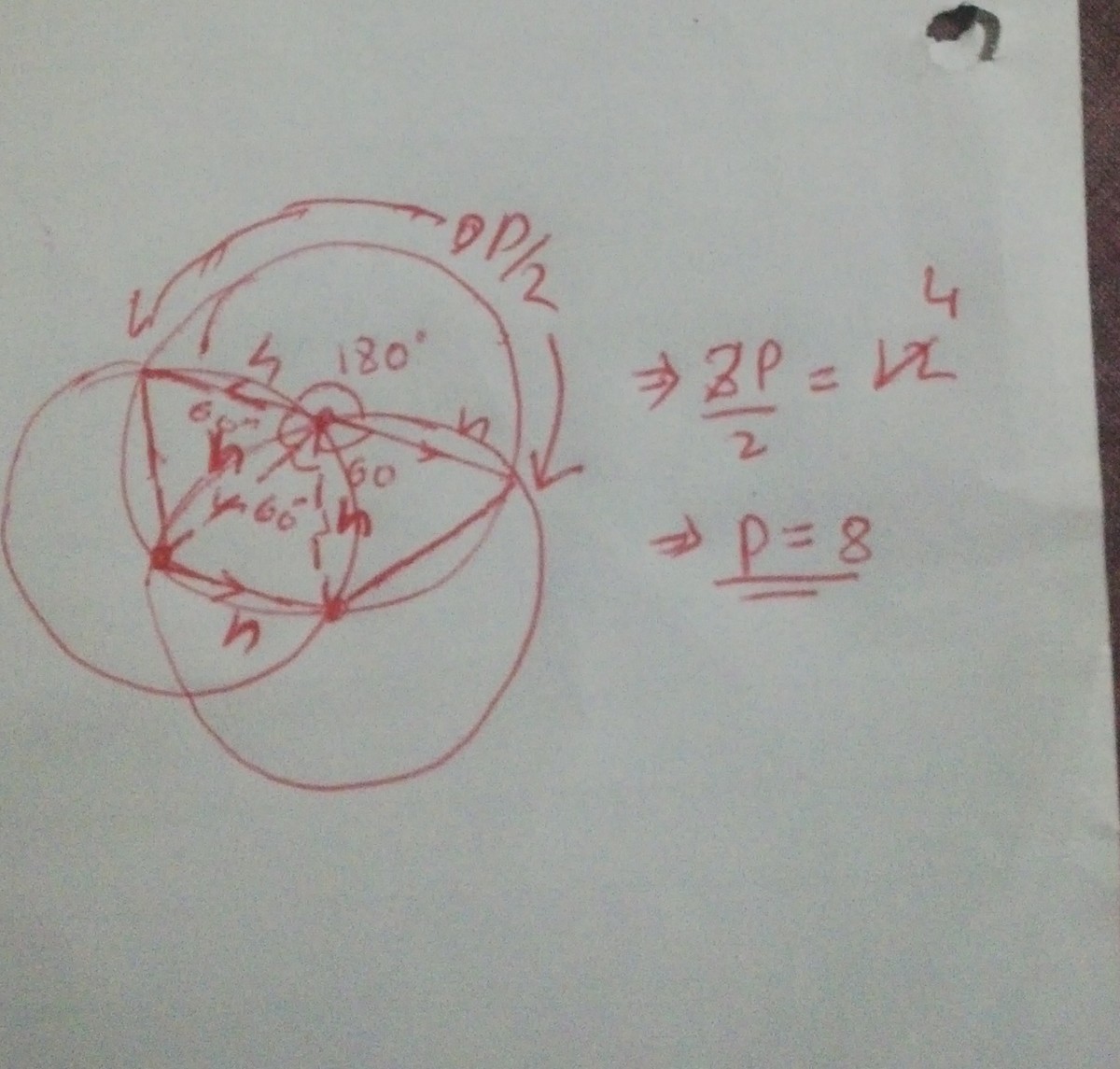
So Δ P F B , Δ P B D , Δ P G D are equilateral.
Therefore angle G P F = 1 8 0
So Arc FG is a semicircle of perimeter 3 1 × 1 2 = 4
Therefore the circumference of any one of the 3 identical circles is 8 .