Path Length in a Binary Tree
A full binary tree of height 4 has 15 nodes, as pictured below.
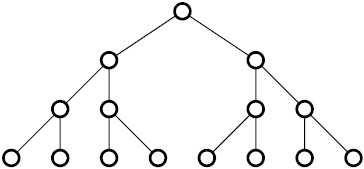
The 8 nodes at the bottom of the tree are called end nodes or leaf nodes. Two distinct end nodes are uniformly chosen. The expected length of the shortest path between them can be expressed as b a , where a and b are coprime positive integers. What is the value of a + b ?
The answer is 41.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
17 solutions
The two end nodes can either be separated by one, two, or three levels. The total possible combinations of end nodes is ( 2 8 ) or 28. Those separated by one level (thus having a path length of two) can occur in 4 ways. The probability of being separated by one level is thus 2 8 4 .
Those separated by two levels can occur in 8 ways. Looking at one 2nd level branch, one node must be picked from the left and one from the right. The two options on the left times the two on the right yields 4, which for the two 2nd level branches yields 8. The probability of being separated by two levels is thus 2 8 8 .
For end nodes separated by three levels, multiply the 4 end nodes on the right by the 4 on the left to get 16 total possible combinations. The probability of being separated by 3 levels is thus 2 8 1 6 .
The shortest path length for 2 nodes separated by n levels is 2 ∗ n ∗ . The expected length of the shortest path is a weighted average, multiplying the probability of each path length by that path length. So in this case, it is 2 × 2 8 4 + 4 × 2 8 8 + 6 × 2 8 1 6 = 7 3 4 . Therefore, a + b = 4 1
Note that the total number of possible combinations is ( 2 8 ) = 2 8 .
Starting with the far left node, we list out the lengths of each path from it to every other node. They are 2 , 4 , 4 , 6 , 6 , 6 , 6 .
We then proceed to the second to left node, listing out paths from it to every other node except for the leftmost node, as it has already been counted. We get 4 , 4 , 6 , 6 , 6 , 6 .
We repeat this for every node until we reach the last node, and we have 2 , 6 , 6 , 6 , 6 , 6 , 6 , 6 , 6 , 2 , 4 , 4 , 4 , 4 , 2 .
We add up all the numbers, obtaining a result of 1 3 6 , and as we are calculating expected value we divide by the total probability, 2 8 , and we get 2 8 1 3 6 = 7 3 4 . We then add together 3 4 and 7 and get a final answer of 4 1
First, we note that any end node will do for our starting point, as they are indistinguishable from one another. We then proceed with casework, considering each case in order. In this problem, our cases will be how many levels we must go "up" to start going "down" toward our chosen end point.
As an example, consider the case where we have to go up two levels. In this case, we have two possible end nodes; the third is discounted by noting that we only had to go up one level to get to it. The probability that we pick one of these two possible end nodes is 2/7, and the shortest path length to get to these nodes is 4. Thus, (2/7) * 4 will become the second term in our expected value equation.
Using this method with the possible three cases, we find that our expected path length is equal to (1/7) * 2 (one level up) + (2/7) * 4 (two levels up) + (4/7) * 6 (three levels up). Simplifying, we get that our expected path length is 34/7.
The original problem asked for the sum of our numerator and denominator, so we add 34 + 7 to get 41 as our final answer.
After choosing the first node (from 8 different nodes) randomly . We always have 7 different choice for the second node (as the two nodes are distinct) .If we choose these 7 nodes one by one then the shortest distance between the two nodes are always ( 2,4,4,6,6,6,6 ) .
so the average is {(2+4+4+6+6+6+6) / 7} = 34 / 7 thus, 34 + 7 = 41
Without loss of generality, start at the leftmost leaf.
The sum of all path lengths to the other leaves is then 2(1 1 + 2 2 + 3*4) = 34, and the mean path length is therefore 34/7, making the requested number 34 + 7 = 41.
In general, for a complete tree of height N, the mean path length between leaves would be
(1 2 + 2 4 + 3*8 + ... + (N - 1) * 2^(N - 1)) / (2^(N - 1) - 1)
= 2 ((N - 2) * 2^(N - 1) + 1) / (2^(N - 1) - 1)
(which you can prove by induction mathematics).
The distance between two distinct end nodes is equal to the distance traveled up the tree plus the distance traveled down. To minimize this, we only travel up until reaching the first node that contains both nodes. The distance is then equal to 2*upwards movement. For any end node, there are 2 n − 1 destination nodes under the node n units up from the original. Since there are 7 possible destination nodes with equal probability of being chosen, the expected value becomes the sum of 7 1 × 2 n − 1 × n , for each n , in this case n = 1 , 2 , 3 . Summing gives 7 3 4 = b a , a + b = 4 1 .
[Latex edits - Calvin]
Without loss of generality we can pick any of the leaf nodes to be the first node chosen. For the second node to be chosen there are 7 remaining options. Only one of those will have a path length 2, 2 of them will have path length 4, and 4 of them will have path length 6. This gives us the expected length of the path to be L = 1 / 7 ∗ 2 + 2 / 7 ∗ 4 + 4 / 7 ∗ 6 = 3 4 / 7 . Since 34 and 7 are already coprime we get the answer is 3 4 + 7 = 4 1
If the first end node is chosen, then it can go to the second node in 2 lines, third and fourth node in 4 lines, and the last four nodes in 6 lines. Similarly we can see that there will be 4 "2 lined paths", 8 "4 lined paths" and 16 "6 lined paths.
So average of paths= 4 + 8 + 1 6 4 ∗ 2 + 8 ∗ 4 + 1 6 ∗ 6 = 7 3 4 so the answer is 41.
note that the net path length from a given point to all the rest is unchanged irrespective of where the node is.Also note that we must divide by 2, as each path has 2 points.So,
expected path length is:-
( {( 2+4+4+6+6+6+6)}
8)/(({8 \choose 2})
2)=34/7
There are 8 7/2= 28 pairs of distinct end nodes. In 4 of these pairs the end nodes are at distance two, in 8 of these pairs the end nodes are at distance four and in 16 of these pairs the end nodes are at distance eight. So, the expected length is 2 (4/28) + 4 (8/28)+6 (16/28)=34/7.
Suppose we choose two leaf nodes. We have three cases: -The leaves share the same parent. The length is 2, there are 4 pairs of such nodes. -The leaves' parents share the same parent. Then, we have 8 pairs, with length of 4 between each. -The root node is the first common ancestor. We have 16 of these, with length 6.
Thus the expected value is $2\cdot\frac{4}{28}+4\cdot\frac{8}{28}+6\cdot\frac{16}{28}=\frac{34}{7}$. Therefore, our answer is $34+7=\box{41}$.
There is a 4/7 chance that you have to go a full length of 6 making 24/7
There is a 2/7 chance that you have to go a length of 4 making 8/7
There is a 1/7 chance that you have to go a length of 2 making 2/7
24/7+8/7+2/7=34/7
34 and 7 are coprime
34+7=41.
Let X be the random variable describing the path length from one node to another node. By definition, the mean of X is given by μ x = ∑ i 7 L i where L i is the length of the path to node i and divided by 7 because there are 7 other bottom nodes besides the selected node.
Starting with the node in the bottom left, the mean, or expected, path length to all other nodes is 7 1 ( 2 + 4 + 4 + 6 + 6 + 6 + 6 ) = 7 3 4 . It can easily be shown that the mean for each starting node is equal to 7 3 4 , and thus the expected path length for any node is 7 3 4 . 3 4 + 7 = 4 1
Assuming the leftmost end node as the first selection and summing up the distances of all the 7 other end nodes, we get the sum as 34. Also, from any other end node, the sum of the distances comes out to be 34. Taking the average distance between two end nodes, we get \frac {34}{7} . Hence, we can conclude that the average distance between two end nodes is also the expected length of the shortest path.
By symmetry, we can assume the first node chosen is the leftmost. There is 1 node for which the shortest path length is 2, there are 2 nodes for which the shortest path length is 4, and 4 nodes for which the shortest path length is 6. Therefore, the expected length is
7
1
(
2
)
+
7
2
(
4
)
+
7
4
(
6
)
=
7
3
4
.
Then
a
=
3
4
,
b
=
7
, and
a
+
b
=
4
1
.
The sum of all path lengths to the other leaves is then 2 ( 1 × 1 + 2 × 2 + 3 × 4 ) = 3 4 , and the mean path length is therefore 7 3 4 , making the requested number 3 4 + 7 = 4 1 .
Without loss of generality, suppose the first node chosen is the leftmost. Working left to right, we see one node at distance 2, 2 nodes at distance 4, and 4 nodes at distance 6. Thus the expected distance is 7 2 + 2 ⋅ 4 + 4 ⋅ 6 = 7 3 4 so the answer is 3 4 + 7 = 4 1