Path minimizing

Geometry Level 3

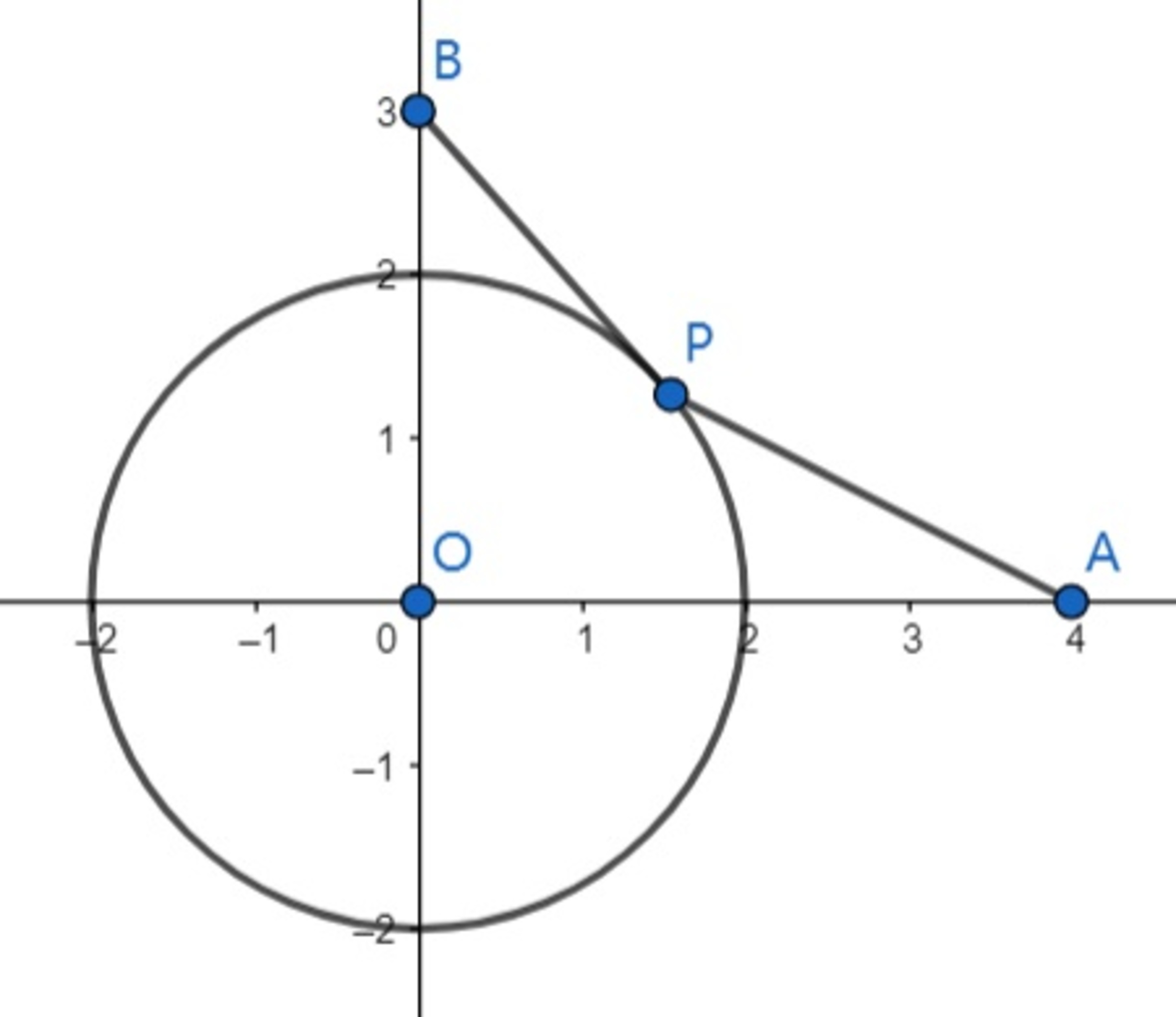
Given $2$ points $A(4,0)$ and $B(0,3)$ on the plane and a point $P$ on the circle $x^2+y^2=4$ .

Find the minimum value of $\frac{1}{2}\overline{PA} + \overline{PB}.$

The answer is of the form $\sqrt{a}$ , please enter the value of $a$ .

The answer is 10.

1 solution

Star Chou
Jul 11, 2018

Let Q be the point lies on the $x$ -axis such that $\triangle OPQ \sim \triangle OAP$ .

Then $\overline{OQ} : \overline{OP} = \overline{OP} : \overline{OA} \implies \overline{OQ} : 2 = 2 : 4 \implies \overline{OQ} = 1$ .

Note that $\overline{PQ} : \overline{AP} = \overline{OP} : \overline{OA} = 1:2$ , we have $\min_P \left \{ \frac{1}{2}\overline{PA} + \overline{PB} \right \} = \min_P \left \{ \overline{PQ} + \overline{PB} \right \} = \overline{QB} = \sqrt{1^2+3^2} = \sqrt{10}.$

There is nothing technically wrong with this problem, except the title is misleading. I thought maybe you had an error and the task was to find the minimum of $\frac{PA+PB}{2}$ since this is more like the path from $A$ to $P$ to $B$ . This answer wouldn't be an integer so there is no risk of getting it wrong.

One way to make the problem more clear would be to make $C$ the midpoint of $\overline{PA}$ then minimize $\overline{PC}+\overline{PB}$

I do like the problem and your clever solution which avoids calculus.

Jeremy Galvagni - 2 years, 11 months ago

Path minimizing

The answer is 10.

1 solution

0 pending reports