Path Up A Mountain
The parks service would like to construct a path that starts at point A and revolves around the mountain once before ending at point B .
Which describes the uphill/downhill nature of the shortest possible path?
Note: Point A is at the base of a mountain in the shape of a right circular cone. Point B is located on the segment between point A and the summit.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Some one asked me a similar question related to cone. But it was about shortest distance between two points on cone. There is a beautiful solution. Cut the cone in such a way that it looks like a sector of a circle. Then joint the two points. We cannot do this for general surfaces. We need tools like calculus of variation or elementary differential geometry. Thanks for the nice solutions by the problem solving group members.
Your path for the obtuse-angled flattened cone does not go around the cone even once - it just goes up and down. As I point out in the second half of my proof, there is no shortest path in this case - the path you show can be thought of as an infimum path instead of a minimal path.
Log in to reply
Do you mean the path in which the sector is ≥ 1 8 0 ∘ ? You can revolve around the cone by passing around the summit (at some arbitrarily close distance to the summit). But you're right, it is impossible to obtain a minimum-length path because for any given path, there will always be a shorter path.
Mathematically the solutions are fine. However, we have to accept that the normal shortest path involves climbing the hill directly, making the revolution at the top before descent back to point B.
The direct line that avoids the summit requires a slope of over 60 degrees.
Log in to reply
I'm not sure what you mean by, "The direct line that avoids the summit requires a slope of over 60 degrees."
Log in to reply
Just pointing out that hills in the real world look more like your 3rd diagram.
You are right that for there to be a shortest path other than the one that loops round the vertex, the semi-vertical angle has to be less than 3 0 ∘ , so the angle of slope of the hill (the angle of elevation of the apex from the base) must be at least 6 0 ∘ . The diagram that goes with the problem is therefore misleading.
Happily, while few conical hills in the world are this steep, mathematicians can still study the spiky conical hills, which give us a more interesting solution that the normal flatter ones!
could u pls explain the 3rd diagram and the reasoning behind it pls!!!!!
Log in to reply
The third diagram is a net of the lateral surface of a cone. If you join the two straight segments, you end up with a cone (without a base). In this case, the angle of the net is greater than 1 8 0 ∘ .
We're trying to find the shortest distance between A and B on this net. To do that, you simply draw a segment up to the top of the cone (along the straight edge of the net), then another segment back down to B (along the other straight edge of the net). In order to fully revolve around the cone, you would have to do a short walk around the summit before going back down again.
It can seem kind of trivial to simply walk up the mountain and then back down again, but this is the shortest path that meets the requirements (because it is the shortest path on the net). Any other path around the cone will be longer.
Suppose that the cone has height H and semi-vertical angle α , that A is at height z = 0 , while B is at height z = H ( 1 − u ) , where 0 < u < 1 . The radius of the cone at height z is given by the formula r = ( H − z ) tan α , and so the position vector of a point on the cone is r = ⎝ ⎛ r cos θ r sin θ z ⎠ ⎞ = ⎝ ⎛ ( H − z ) tan α cos θ ( H − z ) tan α sin θ z ⎠ ⎞ A curve on the cone which passes from A to B after one circuit of the hill is given by some function z = z ( θ ) , where z ( 0 ) = 0 and z ( 2 π ) = H ( 1 − u ) . On this curve, d θ d r = z ′ ( θ ) ⎝ ⎛ − tan α cos θ − tan θ sin θ 1 ⎠ ⎞ + ( H − z ( θ ) ) ⎝ ⎛ − tan α sin θ tan α cos θ 0 ⎠ ⎞ and so d θ d s = sec 2 α z ′ ( θ ) 2 + tan 2 α ( H − z ( θ ) ) 2 = sec α z ′ ( θ ) 2 + sin 2 α ( H − z ( θ ) ) 2 where s is the arc-length, and so the length of the curve from A to B is S [ z ] = sec α ∫ 0 2 π z ′ ( θ ) 2 + sin 2 α ( H − z ( θ ) ) 2 d θ Using the Calculus of Variations, the curve of shortest arc-length satisfies the equation d θ d ( ∂ z ′ ∂ F ) − ∂ z ∂ F = 0 where F = ( z ′ ) 2 + sin 2 α ( H − z ) 2 Since F does not depend explicitly on θ , a first integral of this equation is that z ′ ∂ z ′ ∂ F − F = − ( z ′ ) 2 + sin 2 α ( H − z ) 2 sin 2 α ( H − z ) 2 is constant. Thus we deduce that ( z ′ ) 2 + sin 2 α ( H − z ) 2 = k 2 sin 4 α ( H − z ) 4 for some constant k . Separating variables, this equation becomes ∫ 0 z ( H − z ) k 2 sin 2 α ( H − z ) 2 − 1 d z = ∫ 0 θ sin α d θ = θ sin α The substitution u = sin α ( H − z ) gives − ∫ H sin α u u k 2 u 2 − 1 d u = θ sin α and then the substitution v 2 = k 2 u 2 − 1 gives − ∫ k 2 H 2 sin 2 α − 1 v v 2 + 1 d v = θ sin α Defining the angle β = tan − 1 k 2 H 2 sin 2 α − 1 , we obtain v = tan ( β − θ sin α ) which gives the formula z ( θ ) = H ( 1 − cos ( β − θ sin α ) cos β ) Finally, the requirement that z ( 2 π ) = H ( 1 − u ) tells us that tan β = u sin ( 2 π sin α ) 1 − u cos ( 2 π sin α ) Eliminating β from these equations, we obtain z = H ( 1 − sin ( θ sin α ) + u sin ( ( 2 π − θ ) sin α ) u sin ( 2 π sin α ) ) This solution is valid for values of α for which 2 π sin α < π , so that sin α < 2 1 , or α < 6 1 π .
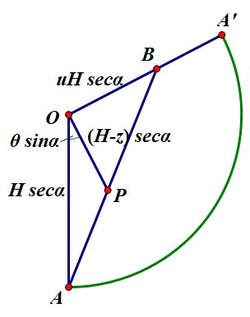 So what is this solution? A more geometric approach to the problem involves rolling the cone out flat to form a sector of a circle
O
A
A
′
. If
H
is the height of the cone and
α
the semi-vertical angle, then the angle at the centre is
2
π
sin
α
. Provided that this angle is less than
π
(so that
sin
α
<
2
1
), the shortest distance on the surface of the cone from
A
to
B
which goes round the hill once is the straight line segment
A
B
. The point
P
on the angle line
A
B
has
O
P
=
(
Z
−
z
)
sec
α
, where
∠
A
O
P
=
θ
sin
α
. Simple trigonometry shows that the above formula is the equation of the line
A
B
.
So what is this solution? A more geometric approach to the problem involves rolling the cone out flat to form a sector of a circle
O
A
A
′
. If
H
is the height of the cone and
α
the semi-vertical angle, then the angle at the centre is
2
π
sin
α
. Provided that this angle is less than
π
(so that
sin
α
<
2
1
), the shortest distance on the surface of the cone from
A
to
B
which goes round the hill once is the straight line segment
A
B
. The point
P
on the angle line
A
B
has
O
P
=
(
Z
−
z
)
sec
α
, where
∠
A
O
P
=
θ
sin
α
. Simple trigonometry shows that the above formula is the equation of the line
A
B
.
If the shape of the cone and the position of B are such that ∠ O B A is acute (the LH diagram below) the distance to O first decreases, and then increases, as we pass along the line segment from A to B . This certainly happens if ∠ A O A ' is obtuse, as in the diagram, but can occur if ∠ A O A ′ is acute. In this case the path first rises, then falls. If, on the other hand, the angle ∠ O B A is obtuse, then the distance to O decreases steadily as we pass from A to B . For this to happen ∠ A O A ′ must be acute. In this case the path rises continually. Thus the path rises continually provided that 2 π sin α < 2 1 π (so sin α < 4 1 ) and cos ( 2 π sin α ) < u . Otherwise the path first rises, then falls.
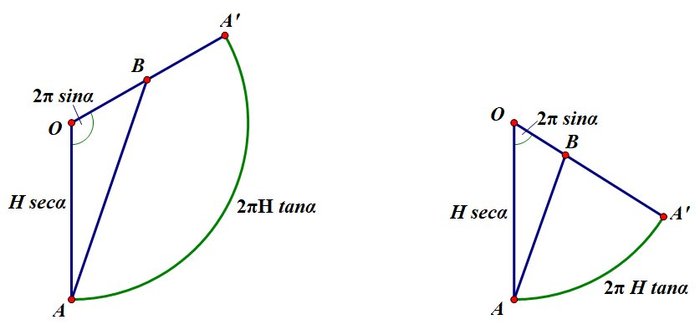
 Finally, what happens if
2
π
sin
α
>
π
? In this case, the unrolled cone is greater than a semicircle, and there is no direct line path from
A
to
B
any more. In this case there is no path of minimum distance that goes round the hill just once. A path that head straight up hill, making an very small detour to dodge
B
on the way up, then circles around the summit in a very small circle, then comes straight down the hill to stop at
B
, will be a path of a length that is greater than
H
(
1
+
u
)
sec
α
. Letting the size of the detours tend to zero yields
H
(
1
+
u
)
sec
α
as the infimum path distance. In this case, the path first rises, then falls.
Finally, what happens if
2
π
sin
α
>
π
? In this case, the unrolled cone is greater than a semicircle, and there is no direct line path from
A
to
B
any more. In this case there is no path of minimum distance that goes round the hill just once. A path that head straight up hill, making an very small detour to dodge
B
on the way up, then circles around the summit in a very small circle, then comes straight down the hill to stop at
B
, will be a path of a length that is greater than
H
(
1
+
u
)
sec
α
. Letting the size of the detours tend to zero yields
H
(
1
+
u
)
sec
α
as the infimum path distance. In this case, the path first rises, then falls.
In summary, the path either rises steadily, or else first rises and then falls. Which happens depends on the shape of the hill and the position of B .
one can even watch ''VSauce " a youtube channel video "which way is down"
Excellent.
I saw a similar problem recently on the mindyourdecisions youtube channel, so I thought I already knew the answer, and immediately guessed without putting any thought into it whatsoever. I was wrong of course! I'm going to read your solution now. It looks tasteful.
One way to think of this is with extreme cases.
- If the cone was extremely tall (pointy), it would be a cylinder in practice. The shortest track here would be to go uphill the entire way, with a constant climb.
- If the cone was extremely short (flat), it would be like a circle in practice. The shortest track would go straight up to the summit, then directly down to B.
The track route therefore must depend on the dimensions.
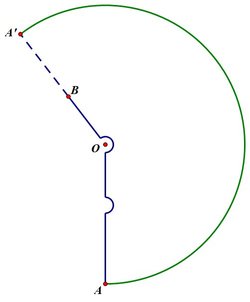
These are two flattened out cones. The first edge is the segment TB. The edge of the skinny cone is TA'. The edge of a fatter, shorter cone is TA.
The dashed lines A'B and AB represent the shortest distance on the cone from A' and A to B. Every point on the curved contours is at an equal height.
The path from A' to B is tangent to the height contour on which B lies. It never crosses the contour; it only goes uphill.
The path from A to B crosses the contour on which B lies. It goes uphill crossing height contours until it reaches the height of the dotted contour, to which it is tangent. Then it goes downhill.
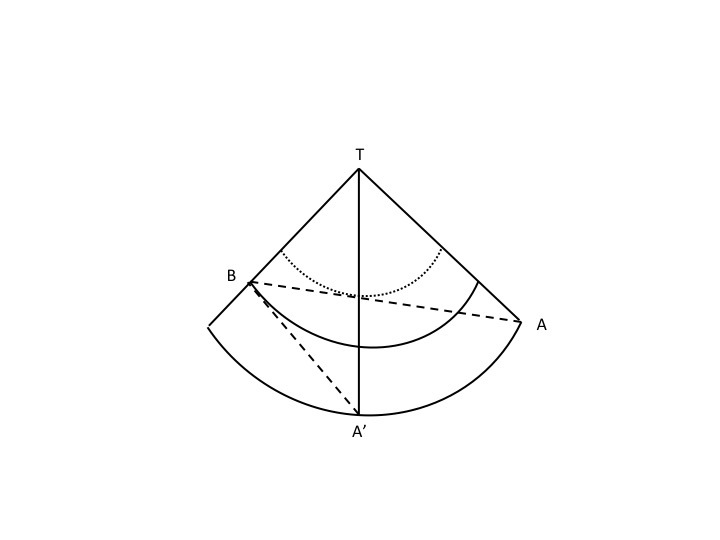
I simply considered the extreme cases of a circle and a cylinder. It is clear that for the circle you would go up to the center, round and back. However, for the cylinder you would go uphill steadily.
The shortest path can be constructed by cutting up the cone along the line connecting the two points and the top, making it flat, and drawing a straight line between the points. To answer the question it is sufficient to look at two possibilities. First, if point B is an infinitesimal distance below the peak. In that case the path is always upwards. Second, if point B is infinitesimal distance above the base. In that case the shortest path will go up first and down later. Therefore the answer depends on the parameters.
The net of the lateral surface of a cone is a circular sector.
We will cut the cone along the segment between A and the summit. We will place point A on one side of the net and point B on the other side.
Consider an obtuse-angled sector. Then, the shortest distance between A and B (revolving around the mountain once) will simply be a straight line on the net.
The path is closest to the summit when it passes through the perpendicular dropped from the summit point. Then the path moves further away from the summit as it approaches B .
In this case, the path goes uphill part of the way, and downhill the rest of the way. This is also the case when our net sector is ≥ 1 8 0 ∘ . To obtain the shortest path that revolves around the mountain once, we simply go straight up the mountain, pass around the summit, and then go back down to B again.
However, it is possible for the path to be purely uphill when the net is acute-angled.