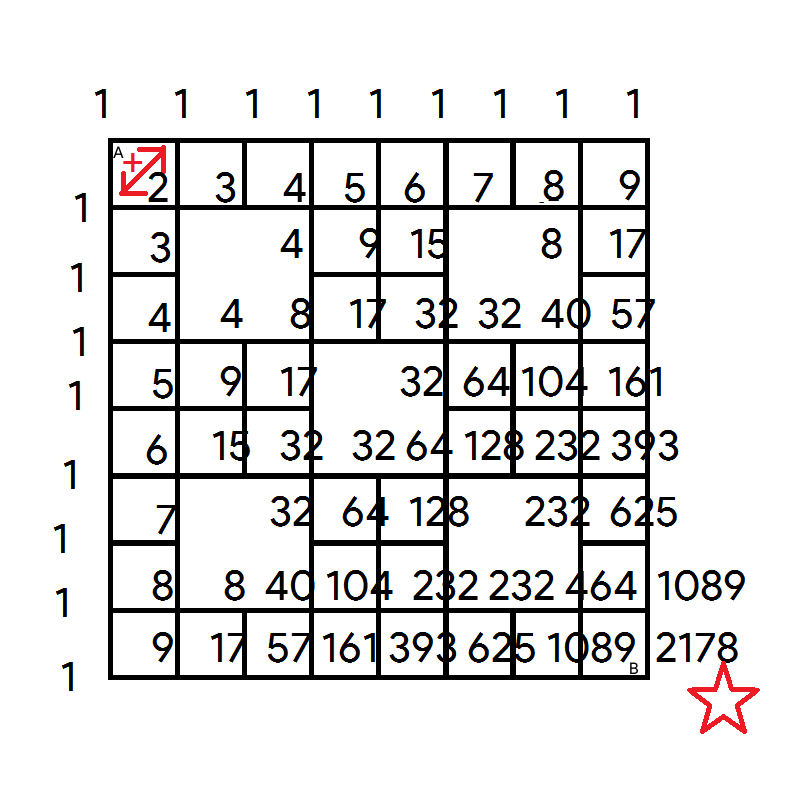
Paths

1st method: Combinatorics method.

Firstly, let's mark the map and fill in the spaces.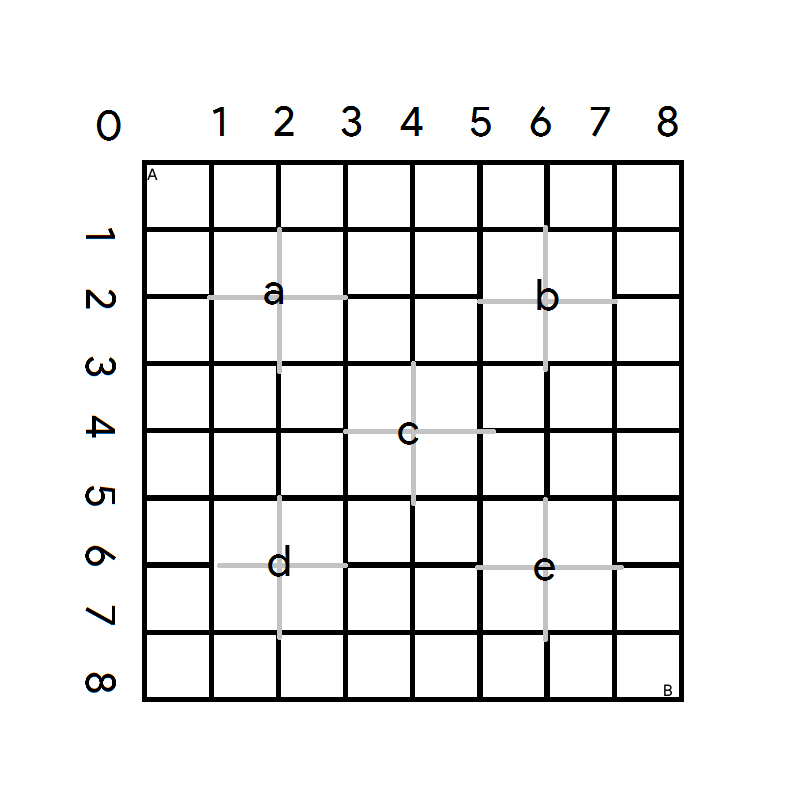 The formula to calculate all the possible paths from $A$ to $B$ without excluding the obstacles is $\begin{pmatrix} m+n \\ n \end{pmatrix}$ for a $m\times n$ grid. $\begin{pmatrix} 8+8 \\ 8 \end{pmatrix}=12870$

Then, we need to calculate the number of paths that pass through the obstacles. The formula to find out the number of paths passing through a point in a $m\times n\$ grid is $\begin{pmatrix} a+b \\ b \end{pmatrix}\begin{pmatrix} \left( m+n \right) -\left( a+b \right) \\ n-b \end{pmatrix}$ given that $a$ and $b$ are the coordinates of the point.

The number of paths that pass through obstacles $a$ and $e=\begin{pmatrix} 2+2 \\ 2 \end{pmatrix}\begin{pmatrix} \left( 8+8 \right) -\left( 2+2 \right) \\ 8-2 \end{pmatrix}=5544\\$

The number of paths that pass through obstacles $b$ and $d=\begin{pmatrix} 2+6 \\ 6 \end{pmatrix}\begin{pmatrix} \left( 8+8 \right) -\left( 2+6 \right) \\ 8-6 \end{pmatrix}=784\\$

The number of paths that pass through obstacles $c=\begin{pmatrix} 4+4 \\ 4 \end{pmatrix}\begin{pmatrix} \left( 8+8 \right) -\left( 4+4 \right) \\ 8-4 \end{pmatrix}=4900\\$

Next, we need to find out the number of overlapping paths between the obstacles. We will be using the same concept.

Overlapping paths between obstacles $a$ and $b$ , $a$ and $d$ , $b$ and $e$ , $d$ and $e$ $=\begin{pmatrix} 2+2 \\ 2 \end{pmatrix}\begin{pmatrix} \left( 2+6 \right) -\left( 2+2 \right) \\ 6-2 \end{pmatrix}\begin{pmatrix} \left( 8+8 \right) -\left( 2+6 \right) \\ 8-6 \end{pmatrix}=168\\$

Overlapping paths between obstacles $a$ and $c$ , $a$ and $e$ , $c$ and $e$ $=\begin{pmatrix} 2+2 \\ 2 \end{pmatrix}\begin{pmatrix} \left( 4+4 \right) -\left( 2+2 \right) \\ 4-2 \end{pmatrix}\begin{pmatrix} \left( 8+8 \right) -\left( 4+4 \right) \\ 8-4 \end{pmatrix}=2520\\$

After that, we will find out the number of overlapping paths in the overlapping paths between the obstacles.

Overlapping paths in the overlapping paths between the obstacles $a$ , $b$ , $e$ and $a$ , $d$ , $e$ $=\begin{pmatrix} 2+2 \\ 2 \end{pmatrix}\begin{pmatrix} \left( 2+6 \right) -\left( 2+2 \right) \\ 6-2 \end{pmatrix}\begin{pmatrix} \left( 6+6 \right) -\left( 2+6 \right) \\ 6-6 \end{pmatrix}\begin{pmatrix} \left( 8+8 \right) -\left( 6+6 \right) \\ 8-6 \end{pmatrix}=36\\$

Overlapping paths in the overlapping paths between the obstacles $a$ , $c$ , $e$ $=\begin{pmatrix} 2+2 \\ 2 \end{pmatrix}\begin{pmatrix} \left( 4+4 \right) -\left( 2+2 \right) \\ 4-2 \end{pmatrix}\begin{pmatrix} \left( 6+6 \right) -\left( 4+4 \right) \\ 6-4 \end{pmatrix}\begin{pmatrix} \left( 8+8 \right) -\left( 6+6 \right) \\ 8-6 \end{pmatrix}=1296\\$

Finally, sum up the numbers.

All paths from $A$ to $B$

$=$ Total number of possible paths from $A$ to $B$ without excluding the obstacles $-$ Total number of paths that pass through the obstacles $+$ Total number of overlapping paths between the obstacles $-$ Total number of overlapping paths in the overlapping paths between the obstacles

$=12870-\left( 5544\times 2+784\times 2+4900 \right) +\left( 168\times 4+2520\times 3 \right) -\left( 36\times 2+1296 \right) \\ =2178$

Note: Some steps have been removed to prevent repetition.

2nd method: Trick method.

Just line up the top side and left side of the map with $1$ 's and add up the numbers on the diagonals. Refer to the diagram below.