Patio blocks
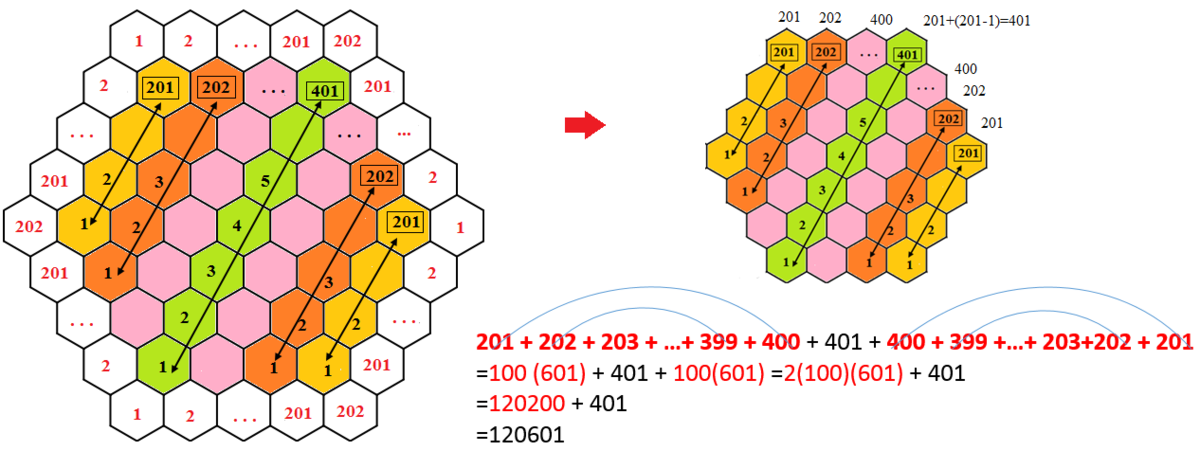
Regular hexagon patio blocks of area 1 are used to outline the garden shown, with n = 5 blocks on each side placed edge to edge.
If n = 2 0 2 , then what is the area of the garden enclosed by the path?

The answer is 120601.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
Very smart!! :)
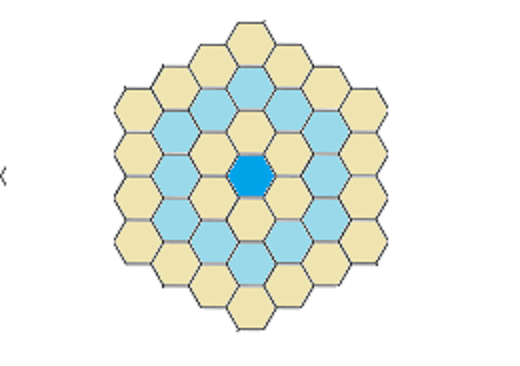
The area enclosed by a ring of hexagons such as given in the question can itself be tiled with similar hexagons, as seen below; the diagram also shows that such an area can be divided into six triangular areas, plus the center tile.
Each triangular area consists of a triangle number T n of tiles. Triangle numbers are just the sums of consecutive integers starting at 1; e.g in the diagram it's easy to see that T 5 = 1 + 2 + 3 + 4 + 5 = 1 5 . In general, T n = k = 1 ∑ n k = 2 n ( n + 1 ) .
In the diagram, the hexagonal area has six tiles on each side, and each triangular area has T 5 tiles. Similarly, in a hexagonal area with n tiles on each side, each of the six triangular areas will contain T n − 1 tiles. Thus a hexagonal area with n tiles on each side will contain 6 T n − 1 + 1 tiles.
If the surrounding ring has 202 tiles on each side, then the enclosed hexagonal area will have 201 tiles on each side; therefore this hexagonal area will contain 6 T 2 0 0 + 1 tiles. So the total area of tiles enclosed by the ring is
6 T 2 0 0 + 1 = 6 [ 2 ( 2 0 0 ) ( 2 0 1 ) ] + 1 = 1 2 0 6 0 1
We note that for an n -block edge path, where n > 1 , there are b n = 6 n − 6 = 6 ( n − 1 ) blocks making the path and that b 1 = 1 . Let the area enclosed by an n -block edge path be A n . We note that A 1 = 0 , A 2 = b 1 = 1 , A 3 = b 1 + b 2 = 7 , and so on, implying...
A n = k = 1 ∑ n − 1 b k = 1 + k = 2 ∑ n − 1 6 ( k − 1 ) = 1 + k = 1 ∑ n − 2 6 k = 1 + 6 × 2 ( n − 2 ) ( n − 1 ) = 3 n 2 − 9 n + 7 for n ≥ 2
Therefore, A 2 0 2 = 3 ( 2 0 2 ) 2 − 9 ( 2 0 2 ) + 7 = 1 2 0 6 0 1 .
@ Chew-Seong Cheong - In your last line, you need to have the closing parenthesis between 202 and the exponent of 2, because you are substituting 202 in parentheses everywhere there is an n.
Log in to reply
3 ( 2 0 2 2 ) ≡ 3 ( 2 0 2 ) 2 ≡ 3 × 2 0 2 2
Log in to reply
That is irrelevant. The fact that those are equivalent does not address what I stated. You are to substitute in by the middle version. That is the correct usage. The exponent falls outside of the parentheses. This would become more apparent if you were to be substituting a negative number, somehow, instead.
Given that n=202. Therefore, the area of the garden enclosed by the path equal to 120601.
The area is a summation of hexagon rings as follows:
Beside the center, the area of each ring is 6* (n -1). So, the areas of the rings from the center outwards are: 1, 6, 12, 18, 24,..., 1200 Which is an arithmetic series (starting from the second ring) and can be calculated as 1 + 200 * (6+1200)/2 = 120601
I like that and the diagram!
Area of round path made up of 5 tiles side will be 5 × 6 − 6 (subtracted 6,because 6 tiles are common at cornors) ,more generaly area of round path of n tiles will n × 6 − 6 . And total area in it will be ( i = 2 ∑ n n × 6 − 6 ) + 1 = 3 n ( n − 1 ) + 1 (added 1 for center tile) . For n=201, 3 ( 2 0 1 ) ( 2 0 0 ) + 1 = 1 2 0 6 0 1
Note that when n = k , the patios for n = k − 1 , k − 2 , . . . , 2 , 1 fit perfectly inside. Further note that the area for the k th layer of patio is A k = 6 k − 6 , since the 6 corners of the hexagon are double-counted and need to be subtracted out.
Since 1 must be added to account for the center hexagon, the total area of the garden enclosed by n = 2 0 2 is:
A 2 0 2 = 1 + n = 1 ∑ 2 0 1 ( 6 n − 6 ) = 1 + 6 n = 1 ∑ 2 0 1 ( n − 1 ) = 1 + 6 n = 0 ∑ 2 0 0 ( n ) = 1 + 6 ⋅ 2 ( 2 0 0 ) ( 2 0 1 ) = 1 + 1 2 0 6 0 0 = 1 2 0 6 0 1
The area of the enclosed garden is six times the triangle number of n -2, plus one.
For n = 5, using the triangle number formula:
a r e a = 2 s × ( s + 1 )
s = n − 2 ⟹ s = 3
2 3 × ( 3 + 1 ) = 6
6 x 6 + 1 = 3 7
For n = 202:
6 × 2 2 0 0 × 2 0 1 + 1 = 1 2 0 6 0 1
Python one liner:
f=lambda n: 1 if n==1 else 6*(n-1)+f(n-1); f(201) 120601
f(n) is total area of hex of side= n unit hexes
Define f(n) recursively and evaluate at 201 because only counting area of internal garden and not outer 202 layer.
The enclosed green area is the sum of series 1+6{(1+2+3+......200)}=120601. This green area is surrounded by 201×6=1206 hexagonal pathway tiles.
In the example the pathway has 4×6=24 hexagonal tiles and the enclosed green area is given by series 1+6{(1+2+3)}=37 tiles.
The longest row in the garden (any that goes from a vertex to the opposite vertex) is 2 n - 3. For n = 202 that's 401. The two rows next to it are one shorter in length, and so on and so on, until the shortest row in the garden (any that goes alongside one patio block edge) is reached, which has length n - 1. The total amount of rows, excluding the longest, is 2((2 n - 3) - ( n - 1)) each with an average length of ((2 n - 3 - 1) + ( n - 1))/2 which means that for n = 202 the total of this area is 2(401 - 201)(400+201)/2 = 120200. Adding the two we get 120601.
I know, this only makes sense for me, but that is how I solved it!
When n = 5 , the blocks enclose 3 7 hexagons of equal area to each of the tiles of area 1 , and so the area of the garden is 3 7 .
It turns out that the number of hexagons in a hexagonal arrangement is always the difference between two consecutive cubes, as shown in the visual below, where the 3 7 blocks that are added to a 3 × 3 × 3 cube to make a 4 × 4 × 4 cube are in a hexagonal arrangement (which shows that the hexagonal number 3 7 is 4 3 − 3 3 ).
This pattern can be extended for any hexagonal arrangement, which means that a hexagonal garden with a side of s is made up of s 3 − ( s − 1 ) 3 blocks. Since the length of the side of the garden is one less than n , s = n − 1 , and so the area of the hexagonal garden with n blocks of area 1 on each side is A = ( n − 1 ) 3 − ( n − 2 ) 3 .
Therefore, when n = 2 0 2 , A = ( 2 0 2 − 1 ) 3 − ( 2 0 2 − 2 ) 3 = 2 0 1 3 − 2 0 0 3 = 1 2 0 6 0 1 .