Patrick's Painting Problem
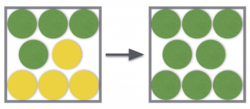Patrick has a box with 4 yellow balls and 4 green balls. He randomly pulls out a ball, and if it is yellow, he paints it green. He then puts it back in the box and continues this process until all of the balls are green. Find the expected value for the number of times Patrick will pull out a ball.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Lets consider how long we expect to take with colouring each yellow ball. The first ball to be painted : we have 4 yellow and 4 green balls therefore our probability of getting a yellow ball is 4/8 or 1/2 as we expect to take 1/probability turns we expect to take 2 turns to get the first ball the second ball to be painted :we have 3 yellow balls and 5 green balls so our probability is 3/8 and we therefore expect to take 8/3 turns to get the second ball . The third ball to be painted : we have 2 yellow balls and 6 green balls therefore our probability is 2/8 or 1/4 and we'd expect to take 4 turns to get the third ball The fourth ball to be painted we have 1 yellow ball and 7 green balls therefore the probability is 1/8 so our expected number of turns is 8
expected number of turns = ((8+4+2)*3)+8) /3 =50/3
hence our answer is 50/3