Pattern Problems!

The first ten terms of any arithmetic sequence is as follows: x, x+d, x+2d, x+3d, x+4d, x+5d, x+6d, x+7d, x+8d, x+9d

The sum of all of these is : 10x+45d The sum of the first five terms is: 5x+10d

The equation goes as follows: 10x + 45d = 4 ( 5x + 10d ) 10x + 45d = 20x + 40d 10x = 5d x = d/2

The ratio of the first term to the second term is : x / x+d When d/2 is substituted in for x, the ratio is : ( d/2 ) / [(d/2) + d]

The simplification goes as follows: ( d/2 ) / [(d/2) + d] ( d/2 ) / (3d / 2) d / 3d 1 / 3

Because the answer is to be given in decimal form, the answer is 0.333.

For calculate the ratio between the first and the second terms, we need to discover the first term and the ratio of the Arithmetic Progression.

According to the informations:

$(A1 + A5) \times 5 \times 4) = (A1 + A10)\times 10$ $(A1 + A5) \times 20 = (A1 + A10) \times 10$

Below, there are the values which satisfy the equation

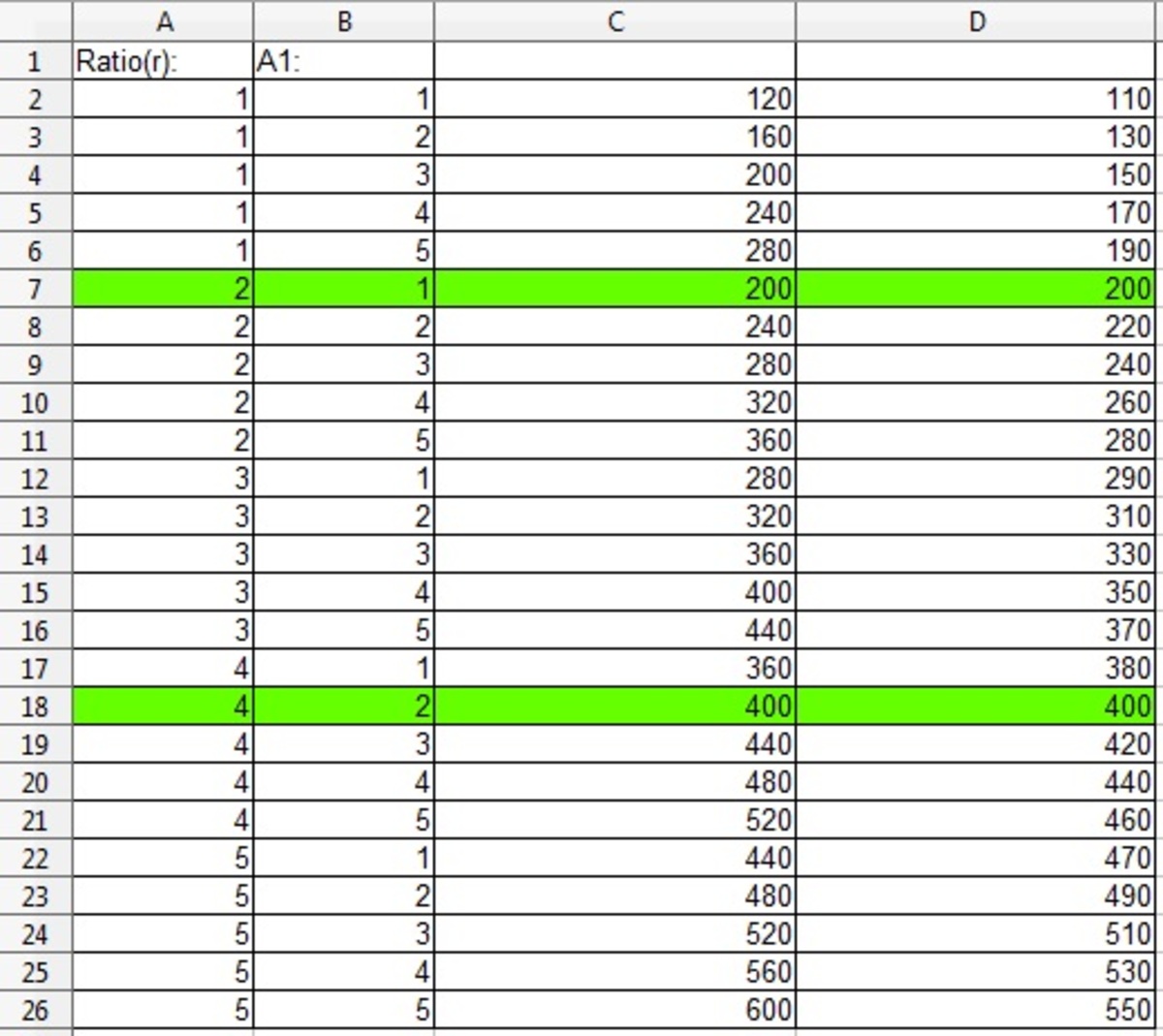
Through the spreadsheet, we discover the values $A1 = 1\ or \ 2$ , and the $\displaystyle A.P \ ratio = 2 \ or \ 4$

Then, the answer is get by $\frac {A1}{A2}$ , such that we use either $A1 = 1$ and $A.P \ ratio = 2$ or $A1 = 2$ and $A.P \ ratio \ = 4$ .

Using the values $1$ and $2$ , calculate the ratio:

$\frac {A1}{A2} = \frac {1}{A1 + r} = \frac {1}{1 + 2} = \boxed {\approx 0.333}$

From S10 = 4S5, we have 5(2a+9d) = 10(2a+4d), where a is the first term, and d is the difference.From that equation we have d=2a. So the ratio of a/(a+d) = 1/3 or 0.333