Peaceful Day on Annulus Court
In the city of Brilliantia, Brilli lives with his family and his pet ant at 360 Annulus Court. Every day, before his neighbors leave for work and school, Brilli must take his ant for a walk. However, he needs to save time on his walk so he has enough time to get to the bus.
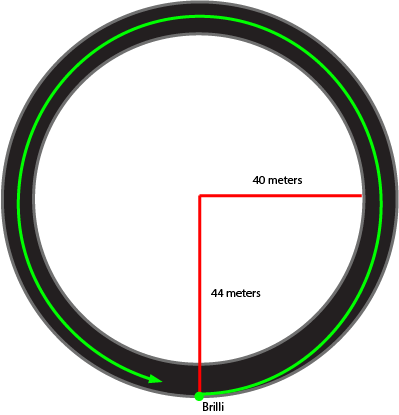
Annulus Court is a perfect annulus, with inner and outer radii of 40 and 44 meters, respectively. What is the length of the shortest path Brilli and his ant can take such that they go all the way around the block?
 Google Maps view of Annulus Court
Google Maps view of Annulus Court
Note : Since no one is driving, Brilli can go on the road as much as he wants. However, he can choose to walk on the sidewalk (gray area) if he chooses.
Bonus : What's the general form for radii and ? Can you prove that it is the shortest path?!
The answer is 253.6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
It seems plausible that we would walk across the street in a straight line tangent to the inner circle and then safely walk around the loop on the inner side of the road, doing the same thing in reverse at the end. The length of this path will be 2 4 4 2 − 4 0 2 + 2 ∗ 4 0 ( π − arccos ( 4 0 / 4 4 ) ) ≈ 2 5 3 . 6 (replace 4 0 by r i and 4 4 by r o to get the general formula.)
It is not hard to see that this is indeed the shortest path. If we write the path in polar coordinates, r ( θ ) , then the length of the long arc between the purple lines is ∫ ( r ( θ ) 2 + r ′ ( θ ) 2 ) d θ , which is minimised when r ( θ ) is held constant, at 4 0 . Furthermore, the points on the purple lines at r = 4 0 are closest to Brilli's initial position.