Peak Voltage
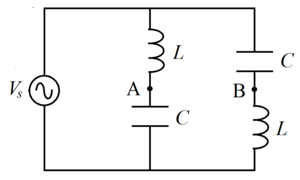
A circuit, consisting of two identical coils each of inductance L , two identical capacitors each of capacitance C , and a variable frequency alternating voltage source with a peak voltage of V s , is connected as shown.
The angular frequency when the peak voltage between terminals A and B , V A B = α V s is given by:
ω = ( α + γ ) L C α + β
Find the sum of constants, β + γ .
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Chew-Seong Cheong Thanks for the solution. Upvoted.
You changed your name. Try to learn up how to draw diagrams. I use Paint. Try to improve writing of problem statements. I have done a few for you already.
Log in to reply
@Chew-Seong Cheong
yes I changed my name.
I will try to improve problem statements. Thanks
Let the angular frequency be ω . The capacitive reactance and inductive reactance is:
X C = − ω C j X L = j ω L
Let the source current be I , the current flowing through A be I A and that through B be I B . The branches A and B are in parallel. Therefore, the equivalent impedance of the given circuit across the source ends is:
Z = 2 X L + X C
Therefore, the current flowing through the source is:
I = Z V S ⟹ I = X L + X C 2 V S
Now, since the branches A and B are similar, one can conclude (and even prove) that:
I A = I B = 0 . 5 I = X L + X C V S
Let the negative terminal of the source be grounded (at 0 V ). Then:
V S − V A = I A X L V S − V B = I B X C ⟹ V A − V B = Δ V = X C + X L V S ( X C − X L )
Plugging in all expressions and computing the modulus of Δ V gives:
∣ Δ V ∣ = ω 2 L C − 1 V S ( ω 2 L C + 1 )
Using the fact that ∣ Δ V ∣ = α V S and solving for ω gives:
ω 2 = ( α − 1 ) L C α + 1
@Karan Chatrath Thanks for the solution.
The peak voltage between A and B is given by:
V A B ⟹ α α − α ω 2 L C ⟹ ω = V A − V B = j ω L + j ω C 1 j ω C 1 V s − j ω L + j ω C 1 j ω L V s = j ω L + j ω C 1 j ω C 1 − j ω L V s = 1 − ω 2 L C 1 + ω 2 L C V s = 1 − ω 2 L C 1 + ω 2 L C = 1 + ω 2 L C = ( α + 1 ) L C α − 1 Multiply up and down by j ω C
Therefore, β + γ = 1 − 1 = 0 .