Peanut Perimeter
The peanut-shaped figure below (in black) consists of four circular arcs with each radius labeled on the dashed segments.
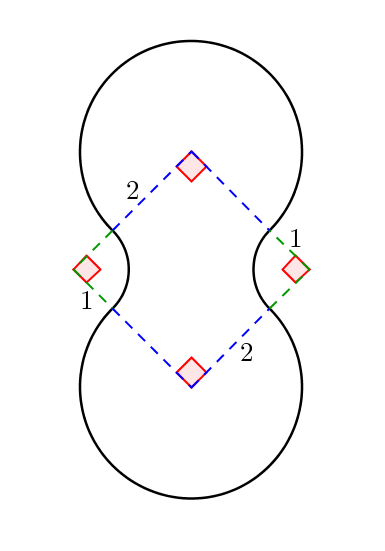
What is the perimeter of the peanut-shaped figure rounded to the nearest whole number?
Note : The blue and green dashed segments are not part of the figure.
The answer is 22.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
If anyone's curious, the area of the peanut is: 2 × ( 4 3 × π × 2 2 ) + ( 9 − 2 1 × π × 1 2 ) = 6 π + 9 − 2 1 π ≈ 2 6
I did not read the problem at first and found the area instead of the perimeter! :P
The circular arcs at the top and bottom are each 4 3 of a circle with radius 2 . The circumference of the whole circle is 4 π , and so the length of each of these arcs is 3 π .
The circular arcs at the left and right are each 4 1 of a circle with radius 1 . The circumference of the whole circle is 2 π , and so the length of each of these arcs is 2 π .
The total perimeter is 7 π .
If you know that π ≈ 7 2 2 , then it is easy to see that 7 π ≈ 2 2 . However, a calculation by hand will also show you that 7 × 3 . 1 4 = 2 1 . 9 8 , which rounds to 2 2 .