Peaucellier-Lipkin Linkage Forces

Classical Mechanics Level 5

This classic mechanical linkage results in a straight line motion of point $C$ as point $A$ is rotated about center $O$ .

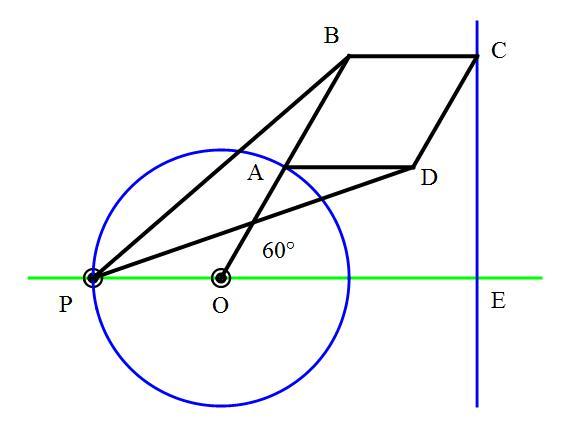
Both points $P$ and $O$ are fixed, as links $PB, PD$ and $OA$ are free to rotate about them.

The lengths of the links are

$OA=AB=BC=CD=DA=1$

while $P, O, E$ are co-linear, and $PO=1$ , $OE=2$ , and $PE\bot EC$

and $PB=PD$

Force $F$ is applied tangentially at point $A$ (perpendicular to $OA$ ), resulting in force $F’$ along the line $EC$ at point $C$ .

At angle $\angle AOE=60°$ , find the ratio of the forces $\dfrac { F }{ F' }$ accurate to three decimal places. As this is an exercise in classical mechanics, use the Conservation of Energy Law to determine this ratio.

Note: A property of Peaucellier-Lipkin linkages is that points $P, A, C$ are always co-linear.

The answer is 2.000.

1 solution

Michael Mendrin
Oct 7, 2015

Since force applied over distance is energy, or $Fd=E$ , and energy is conserved, then we have

$F(OA)d\theta=Fd\theta =F'dx$

where $F$ is tangential force applied at point $A$ over distance $d\theta$ , and $F’$ is the resultant force at point $C$ over distance $dx$ . Because we know that points $P, A, C$ are co-linear at all times, then the position of $x$ as a function of $\theta$ is

$x=3Tan\left( \dfrac { \theta }{ 2 } \right)$

Differentiation then gets us

$\dfrac { dx }{ d\theta } =\dfrac { F }{ F' } =\dfrac { 3 }{ 2 } { \left( Sec\left( \dfrac { \theta }{ 2 } \right) \right) }^{ 2 }$

For $\theta=60°$ , this works out to $2$ , so $F$ is exactly twice that of $F'$

this solution was fantastic!

Γιώργος Σακκάς - 5 years, 8 months ago

Hey why can't I differentiate it two times wrt to time and I will get a relation between $\frac {d^2x}{dt^2} (corresponding to F ' )$ and $\frac {d^2(R* \theta )}{dt^2} (Corresponding to F)$ which also contains the terms of angular velocity of Point A, which can be considered to be 0 in this case..

Moreover don't you think your dimensions are wrong in the energy conservation equation? F*d(theta) does not have the dimensions of Energy if $\theta$ is an angle... You have taken theta to be distance here.. Taking it as the angle would be preferable, But since the value of Radius, R=1 ..The Answer isn't affected. Anyways,

Please reply to why we can't use the method I have written in the first paragraph. Thank You

Jatin Sharma - 5 years, 7 months ago

Radius $OA=1$ , so $OA\,\theta$ has units of length, and force $\times$ length = energy. I've edited my solution so that people will be less confused.

Secondly, this is like how a lever works, but in a more general way. One way to argue how a lever works is looking at it in terms of torque. Another way is to look at the work being done at either end. The latter way makes use of the conservation of energy law.

Michael Mendrin - 5 years, 7 months ago

Thank You I'm getting errors using the torque method, could you help me out please?

Jatin Sharma - 5 years, 7 months ago

Peaucellier-Lipkin Linkage Forces

The answer is 2.000.

1 solution

0 pending reports