Pebble Dragging

Consider the following diagram: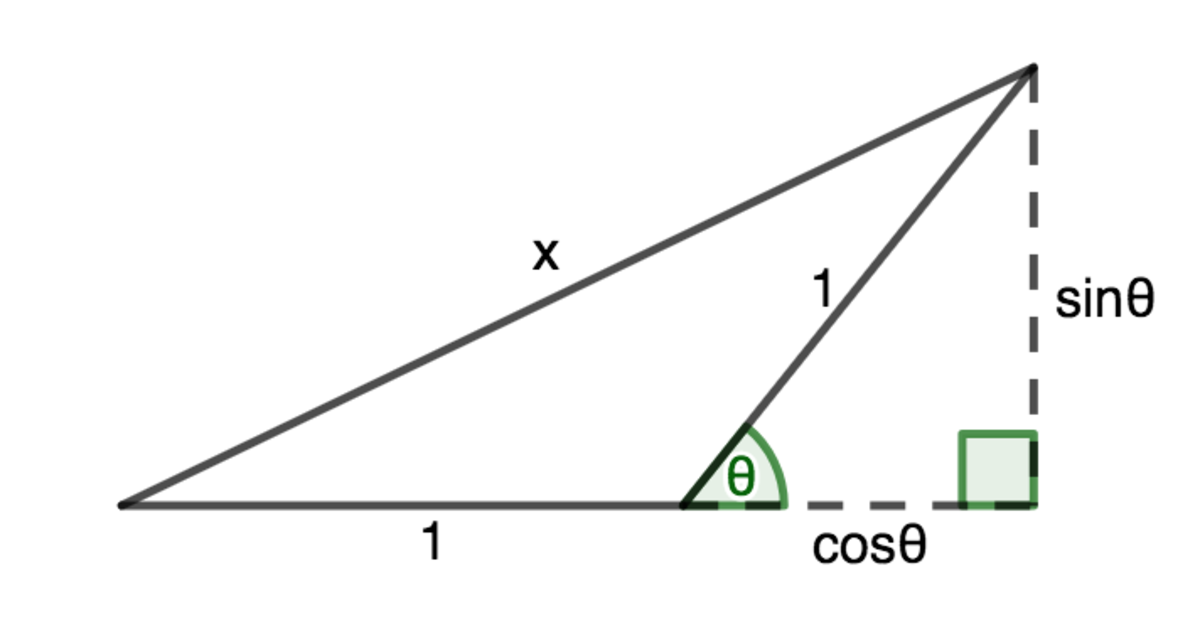 The length x can be found using the Pythagorean Theorem: $x^2 = \sin^2\theta + (\cos^2 + 1)^2 = \sin^2\theta + \cos^2\theta + 2\cos\theta + 1 = 2\cos\theta + 2$ where in the last step we use the trigonometric identity $\sin^2\theta+\cos^2\theta = 1$ . Taking the square root of both sides and applying the double angle identity $\cos2\phi = 2\cos\phi - 1$ yields $x=\sqrt{2\cos\theta + 2}=\sqrt{4\cos^2\left(\frac{\theta}{2}\right)}=2\cos\left(\frac{\theta}{2}\right)$

Now, to find the average value of $x$ , we must find $\frac{1}{b-a}\int_a^bx\,\mathrm{d}\theta$ where $0\leq\theta\leq\frac{\pi}{2}$ . Thus we must evaluate $\frac{1}{\pi/2}\int_0^{\frac{\pi}{2}}2\cos\left(\frac{\theta}{2}\right)\,\mathrm{d}\theta = \frac{2}{\pi}\left[4\sin\left(\frac{\theta}{2}\right)\right]_{\theta=0}^{\frac{\pi}{2}}=\frac{8}{\pi}\left(\frac{\sqrt{2}}{2}\right) = \frac{4\sqrt{2}}{\pi}\approx 1.8$