Pedaling in the mid-air!

Classical Mechanics Level 1

An astronaut stuntman is on a unicycle outside of a space shuttle in Earth's orbit. He jumps from the space shuttle, and as he is falling in space, he starts pedaling.

What will happen next?

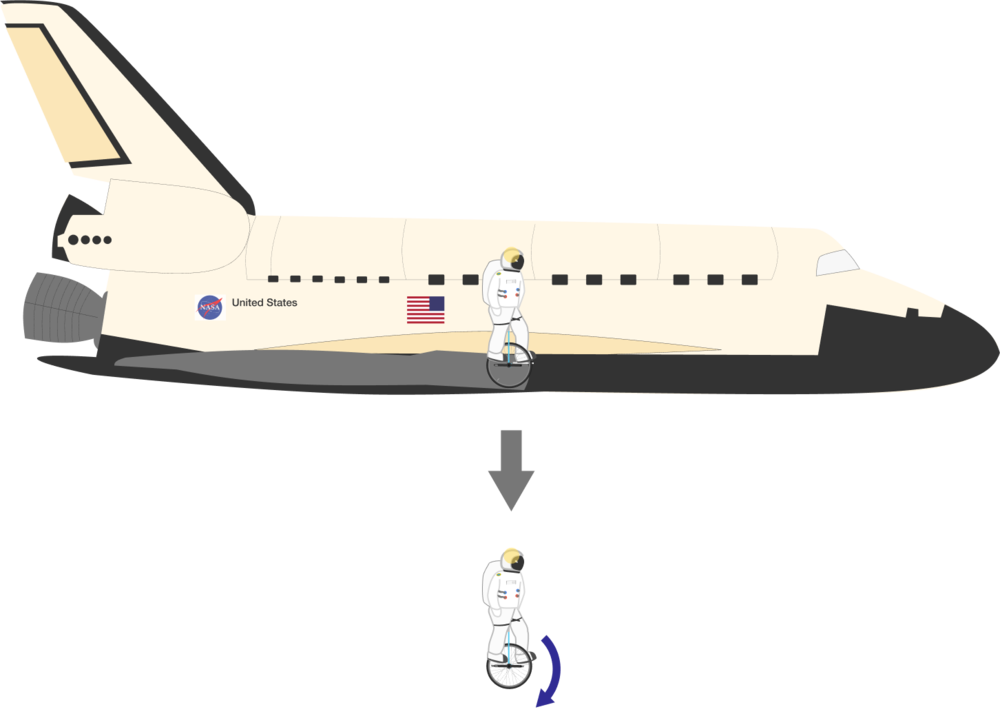
Assume that the astronaut uses their thighs to grip the seat.

The astronaut will spin in the same direction as that of the wheel He'll keep falling without spinning The astronaut will spin opposite to the direction of the wheel

7 solutions

Lucas Viana Reis
Dec 2, 2018

The pedal and wheel have a free degree of motion wheen rotating around their axis. When the stuntman rotates the wheel, the angular momentum of the system must be conserved, so the stuntman therefore has to rotate in opposing direction to that of the wheel.

Also, if you consider the Magnus effect to be strong enough from the fast-spinning wheel, the cycle actually feels a force 'backwards' to that you'd expect if the monocycle were riding on ground.

Edit: things are now on space, so no, no Magnus force. You should only consider conservation of angular momentum.

The wheels of the plane aren’t rotating at all. They are folded up inside the belly of the plane. If they were extended, they would incur the same air pressure as the cycle wheel and therefore respond the same.

Elisa Dowell - 2 years, 6 months ago

Sorry, I said the 'set' but the question has been edited since then. Only the cycle feels the force. Editing it. This is the error you pointed out, right?

Lucas Viana Reis - 2 years, 6 months ago

Newton wins again! Snap! I knew this! cry cry :) So obvious! lol

Alexander Sullivan - 2 years, 6 months ago

interesting

Clack Sam - 2 years, 6 months ago

But why does the unicycle rotate to counter the rotation of the wheel instead of the wheel simply not rotating at all due to the air resistance countering the rotation of the wheel? In other words, what allows us to suppose that the wheel and unicycle are both in the same system?

denis vladu - 2 years, 6 months ago

Denis Viadu, Newton law requires for every action there is an equal and opposite reaction. Also, there will be no air resistance in a low earth orbit.

Alexander Sullivan - 2 years, 6 months ago

What is a “free degree of motion”?

Nathan Pierce - 2 years, 6 months ago

In robotics, a degree of motion or movement is all combinations of movement. A good robot arm would have 4 freedoms. 1) in and out 2) rotate 3) left/eight 4) up/down Hope I am using this example in the proper text.

Alexander Sullivan - 2 years, 6 months ago

The wording in the question text and diagram is rather misleading. The stuntman is in orbit with the space shuttle. He is pictured on the wing. If he were not in contact with the wing he would simply be falling together with the space shuttle, i.e. stay floating next to the space shuttle. He will not fall relative to the shuttle as shown in the picture. Placed as he is on the unicycle in contact with the wing, he cannot "jump" because when he bends his knees to try to jump the wheel will simply lift off the wing and he will stay floating just above the wing. The best he could do would be to press sharply down on the pedals by rotating his ankles. The downward force on the wheel would cause the tyre to be compressed slightly against the wing surface. When it expands back the stuntman would travel upward slowly and be able to perform the pedalling experiment above the shuttle. He would have to use his rocket backpack to return to the shuttle before straying too far.

Dennis Engel - 2 years, 6 months ago

Also you have to think about the weight of the space suit. The back part of of the suit is heavier than the front.

정우 박 - 2 years, 1 month ago

Christian Douctte
Dec 2, 2018

Our system is the stuntman and the unicycle. Lets say we can ignore air resistance. Then, no torque outside the system acts on the system. This means that angular momentum is conserved.

As the total initial angular momentum is 0 (nothing rotating) as the stuntman jumps out of the plane, it must still be 0 when he begins pedaling. Since the wheel is rotating, the stuntman must be rotating in the opposite direction so the total angular momentum can be 0.

Newton’s 3rd Law: “Every action has an equal and opposite reaction” therefore when spinning the unicycle forward, you will spin in the opposite of the direction of the action.

Ryan Lay - 2 years, 6 months ago

How can we ignore aerodynamics in a question with an astronaut! I'm not sure how much it could effect it but I know that the spinning of the wheel will create a pressure differential due to drag and my thought was the unicycle itself will move to the left in this case.But maybe the force is so small it wouldn't matter. Thoughts anyone???

Wade Yeary - 2 years, 6 months ago

In space there is no air (no athmosphere), so air resistance does not exist.

Cristián Infante - 2 years, 6 months ago

Is this just a consequence of newtons third law

Mudit T - 2 years, 3 months ago

Zac Mann
Dec 2, 2018

Due to conservation of angular momentum, rotating the wheel will result in the unicycle rotating in an opposite direction.

Note: There are some typos with this question.

A unicycle by definition has one wheel (so the answers should read "opposite to the direction of the wheel" etc.)
"In the mid-air" should perhaps be replaced with "in mid-air"

there is no air when they are in orbit (it least approximately 0 air.

Doug Stewart - 2 years, 6 months ago

The question has been changed since I posted this (Originally the unicycle was exiting an aeroplane not a shuttle). Regardless, the grammar mistakes are still there.

Zac Mann - 2 years, 6 months ago

Let me dumb it down for my ppl. Say your at the bottom of a swimming pool underwater. Ok to go up you have to push down. On a unicycle in space if you push the pedal clockwise you will go counter clockwise. Simple

Oneal Baptiste - 2 years ago

Zoki Kuzmanovski
Dec 3, 2018

This gif should be helpful, just replace the visualization of a ball with wheels.

Arie Roos
Dec 8, 2018

It made sense for me from the perspective of Newton's 3rd law. If the Astronaut exerts a force on the wheel to get it spinning in one direction, the wheel will exert a force on the astronaut in order to spin him in the opposite direction.

Suvansh Nain
Dec 8, 2018

Simply Newton's 3rd law implies here when we strike the pedal it reacts and applies a force on us spinning us in opposite way

J L
Dec 5, 2018

None of the offered solutions are correct. Uni cycles do not have wheel s .

You're right. I've updated the options to reflect this.

In the future, if you have concerns about a problem's wording/clarity/etc., you can report the problem. See how here .

Brilliant Mathematics Staff - 2 years, 6 months ago

Also, if the astronaut and the shuttle are orbiting the earth, the astronaut is not going to fall (with respect to the shuttle) at all.

Nicola Gabbia - 2 years, 3 months ago

The shuttle and the astronaut both will orbit the Earth, however, their state of motion is still called a free fall as the only force acting on them is the gravity of the Earth.

Rohit Gupta - 2 years, 2 months ago

Pedaling in the mid-air!

7 solutions

0 pending reports