Pencils and Jars
 I have some pencils and some jars.
I have some pencils and some jars.
If I put 4 pencils into each jar, I will have one jar left over.
If I put 3 pencils into each jar, I will have one pencil left over.
How many pencils and how many jars do I have?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
47 solutions
even better is guessing by taking the multiples of 4, in which 3 is a factor of them leaving reminder as 1. example starting from 12. and next number is 16. too simple to understand. Equations everrybody cannot keep in the same way as discussed.
check the options.. that's it!
You meant x - 1 = 3y, But wrote x - 1 = 3 Just saying
Sorry I am bit confused, isn't x-1=3 supposed to be x-1=3y. The solution is great though, nicely done. :D
Log in to reply
Obviously a typo, should be x-1=3y. Isolating the variable x in each equation and substituting each value of x against itself in an equation you find the value of y. Substitute the value of y into one of the equations to get the value of x. Great eye Qi, and great solution Katie
I agree but then if you try once more to get only y you go back to the start: y=(x-1)/3 so i guess that you do can put the equation in the way ×-1=3 That way you do can solve the equation
I thought so too... I only figured it out by looking at the choices and seeing which one worked.
THX <3 I GUT IT <M<<<<<<
You forgot to put 3y
one can do it mentally but this is the right approach ...nice job katie
great one.
when 4 pencils are in each jar then 4of 4 pencils=16 pencils and only one jar is left
Ahh how nice.. :)
thank you for your solution
good explanation . thnks
look options,that's all
Just take the 2nd eqs from the 1st in steps :)
Can't it be done with permutation
Katie excellent
Thanks for sharing...I love figuring out this type of problem.
Awesome...what formula did you use?
:) got it ... thanxxx
Log in to reply
Hello wasssp
Thanks* :)
there is 16 pencils in the 5 jars. 4X4=16 one jar is remaining 3x3=15 one pencil is remaining simple answer
3*3=9 bro isnt it
Log in to reply
jajajaja good point!!! thinking too fast, mistaking too early....jeje
even better is guessing by taking the multiples of 4, in which 3 is a factor of them leaving reminder as 1. example starting from 12. and next number is 16. too simple to understand. Equations everrybody cannot keep in the same way as discussed.
just like Waqas Khan it is simple to solve..doesn't take much time to think. simply adjusting the number of jars with the number of pencils.
Because 4 options have been given, we can easily eliminate. If we devide 4 pencils in a number of jars and one jar is leftover, the number of pencils must be a multiplier of 4. Therefore, there is only one possible choice, which is 16 pencils and 5 jars.
In this case, there is no need to solve equations.
I actually like your solution :D creative
There are two distinct statements. When there are four pencils in each jar there will be one jar left over. We can say that the number of jars is equal to the number of pencils divided by four plus another one. This can be expressed using algebra: j = (p/4) + 1 (where p = pencils and j = jars) When there are 3 pencils in each jar there will be one pencil left. We now need to calculate how many pencils there are. We can say that the number of pencils will be equal to the number of jars times three plus another one. Using algebra again we have: p = 3j + 1
We have ended up with two linear equations. First rearrange the formula to make j the subject: j = (p/4) + 1 (equation 1) j= (p − 1) ÷ 3 (equation 2). with elimination and subtitution then you will get result p = 16 and j = 5
you can write two equations to solve : ........ y=4(x-1).........&........y=3x+1......... where y is the number of pens and x is the number of jars ........ that reveals :......... x=5........ y=16 .......
This one makes sense. Thanks!
Well here is how i solved it:- Since if you put 4 pencils in each jar , 1 jar is left behind so the no. of jars is odd. Hence, (a) is out. Then since if you put 3 pencils in jar then 1 pencil is left behind and so the no. of pencils is more than a multiple of three and thus (c) is out. Now (b) has 16 pencils and (d) has 19 pencils. However since when you put 4 pencils in each jar then a jar is left so it has to be a multiple of 4 and so (b) fits. Thus the answer is 6 pencils and 5 jars.
16 pencils
16 pencils & 5 jars!! 16/4 then 1 jar is left now 16/3 then 1 pencil is left . so simple....
This problem could just as easily be drawn out, if you would be willing to take the time.
While there are many explanations using equations, consider this logical approach:
Assume that there are 4 pencils in every jar except 1 jar, as described.
Now, the question asks us to have 3 pencils in each jar, which is equivalent to removing 1 pencil from each jar with pencils.
With this we can put 3 pencils in the empty jar and still have 1 pencil left. This implies that we removed 4 pencils in total and hence the number of jars must be 1 more than that, that is 5 jars.
Now, there are 3 pencils in each jar and then 1 more, that is 16 pencils.
The first statement implies that the number of pencils is a multiple of 4 and only one option fulfils that condition and when double checked for the second statement that indeed is the answer. In the absence of multiple choice answers one can easily do it either by simultaneous equations or by hit and trial.
Let x be the number of pencils and y be the number of jars.
//If I put 4 pencils into each jar, I will have one jar left over.// If we rephrase this statement to mathematical equation we can state:
x /4 = y-1
then, //If I put 3 pencils into each jar, I will have one pencil left over.// become:
(x-1)/3= y
then we can multiply both equation by two different integers to remove one variable.
using simple algebra, Equation 1 become: x=4(4y-1) x=4y-4
And Equation two become: x=3y+1
So, we use 3 and 4 to remove the variable y.
3(x=4y-4) 4(x=3y+1)
if two equations added, it'll become: -x=-16 then x=16
we can now use substitution..
y= (x-1)/3 y=((16)-1)/3 y= 5
if among 5 jar each jar contains 4 pencils then 16 pencil and one jar left ... and among 5 jars if you distribute 3 in each then 15 pencil get its place but one is left among 16... so 16 pencils and 5 jars
This is how I approached the problem:
1) If I put 3 pencils into each jar, I will have one pencil left over.
So, the number of pencil is some multiple of 3 plus 1. e.g 4,7,10,...
2) If I put 4 pencils into each jar, I will have one jar left over.
So, the number of pencil % 4 = 0 bcs, no pencil left over
Finding the LCM of (x3 + 1 and x4) = 16 pencils
Going back to :
2) I will have one jar left over
Thus the number of jars = 4 1 6 +1 = 5 jars
16 is the only option divisable by 4
I wrote out some multiples of 4 and 3:
4 8 12 16 20
3 6 9 12 15
When 3 pencils are placed in each jar, there is one left over, so I found two multiples which had a difference of 1. These were 16 and 15. I knew this was the answer because the multiples are 1 apart (4 * 4 and 5 * 3) so they were one 'jar' apart.
So if you guys don't want complex equations to solve this question use the "trial and error " method just as I did it. You'll naturally find the fourth option viz 5 jars and 16 pencils!! 😊
That means, I have X jar.
When 1 jar left over, Then I have =4(x-1) pencils.
Again, When 1 pencils left over, Than I have = 3x+1 pencils.
So That, 4(x-1)=3x+1 => 4x-4 =3x+1 => x = 5
So, I have 5 jars & I have (3*5+1)=15+1 =16 pencils.
Simple, the amount of pencils had to be a number of 4 so the only option was 16 pencils
Let there be x pencils & y jars. 1st case: x/4 + 1= y 2nd case: (x-1)/3=y Solving, we get, x=4 and y=5
Let's No. of jar is n And No. of pencil is m At 4 m=4(n-1), At 3 m=3n +1, 3n+1=4n-4, then n=5 jar & m=16 pencil
There could, indeed, be an infinite number of pencils and an infinite number of jars. But, given the four options as possible solutions, the simplest approach is to eliminate the options that do not conform to the logistics of the stated problem. In that case, the only correct option is 16 pencils and 5 jars. If no options were stated for solutions, then multiples of the correct solution would be equally valid, causing an infinite number of pencils and jars.
Suppose there are 5 jars . in each jar i put 4 pencils . 1 jar is left .. Therefore 4+4+4+4 = 16. And there is a option of 16 pencils . and thats the answer .
jars minus 1 can divide for 4 pencils minus 1 can divide for 3 -> look at the answer we got 16 and 5
I first observed that if four pencils were put into four jars that means one jar is left over. That means the amount of pencils is a multiple of four.
The only answer which has the amount of pencils being a multiple of four is : There are 16 pencils and 5 Jars.
4×4=16 pencils left one jar and 3×5=15 pencils left one pencil
Pensils = 3 * Jars + 1Pensils ===> by putting jars=5 , so pensils=16
Looking at the answers, we see that the only answer where the pencils are divisible by 4 is 16 pencils, thus the answer.
Let there by n jars. So, 4(n - 1) = 3n + 1
4n - 4 = 3n + 1
n = 5
No. of jars = 5
Total pencils = 3n + 1 = 16
X=4Y-4;X=3Y+1 simply solve two equations ..X=16 &Y=5
When I read the question without looking at the answers my first way of working it out was right 😋
Idiots, there are infinite pencils and infinite jars
If 4 pencils are put into jars nothing is left ,so no.of pencils is a multiple of 4. And if 3 pencils are put into each jar one is left ,so no.of pencils one more than the multiple of 3. Now, looking at the options 16 is the only number which is multiple of 4 and one greater than multiple of 3
It's easy to guess if the choices are shown. Otherwise, Katie's solution is the right approach.
Well instead of calculating eqs. U shud just look at options carefully
My idea was:
1(mod 4) for jars 1(mod 3) for pencils
When 16 is divided by 3, the remainder is 1 (3 x 5 = 15, 1 remainder). When 5 is divided by 4, you get 1 remainder (4 x 1 = 4, 1 remainder).
Thus, I got 16 pencils and 5 jars.
See all option for such problems It solve........ simple!
4*4=16 is 4 jars and each jar 4 pencils. Remains 1 jar empty
from the multiple answers, minus one jar and then remaining jars multiply with 4 pencils. then we got the total pencils..then we get the correct ans as 16 pencils and 5 jars..
In all of the given options, check for which number of pencils P is
P
≡
0
(
m
o
d
4
)
The only answer satisfying it is 16 pencils and 4 Jars. Which is the correct answer :D
get the lowest factor of 4 that if you divided it to 3 you'll get remainder 1, which is 16 the number of pencils and divide it to 3 and you'll get 5 the number of jars
Let x equal the total number of jars.
If you put 4 pencils into each jar and have one jar leftover, the expression for the total number of pencils would be: 4(x-1) , where (x-1 ) equals the total # of jars minus the one remaining
If you put 3 pencils into each jar with one pencil leftover, the expression for the total number of pencils would be: 3x + 1
Set both to each other:
4(x-1) = 3x + 1 x =5 jars
Plug in x = 5 jars to either side of the equation, and you'll get 16 pencils!
When I take the pencils in groups of 4 of them I know that the number of pencils is a four multiply, and if I take the pencils in groups of 3 the number of pencils is a three multiply plus one, then I have: 4 x = 3 y + 1 Now by the first sentence I know that the number of jars is: 4 4 x + 1 = x + 1 Then by both of sentences I know that the number of jars I will use when I take the pencils in groups of four is one unity larger than when I take them in goups of 3, because in the first case I left one jar over and blah blah blah, so: y = x + 1 Now i have: 4 x = 3 ( x + 1 ) + 1 4 x = 3 x + 4 x = 4 Then the number of pencils is: 4 x = 1 6 And the number of jars is: x + 1 = 5 Tadaaaaaa!
it will be easier to start with any of the four options and proceed!!!!
For making the solution easy make it in the terms of pencils let the pencil be x and the jars be y
so form first statement 4(y-1)=x ............. eq(1)
here 1 is subtracted because there is only one jar left so total no. of jars i.e. (y-1)
from next statement
here we have one pencil left so our equation is (x-1)/3=y
(x-1)=3y
x=3y+1 ...............eq(2) subtracting both the equations
4y-4=x
-( 3y+1=x)
now
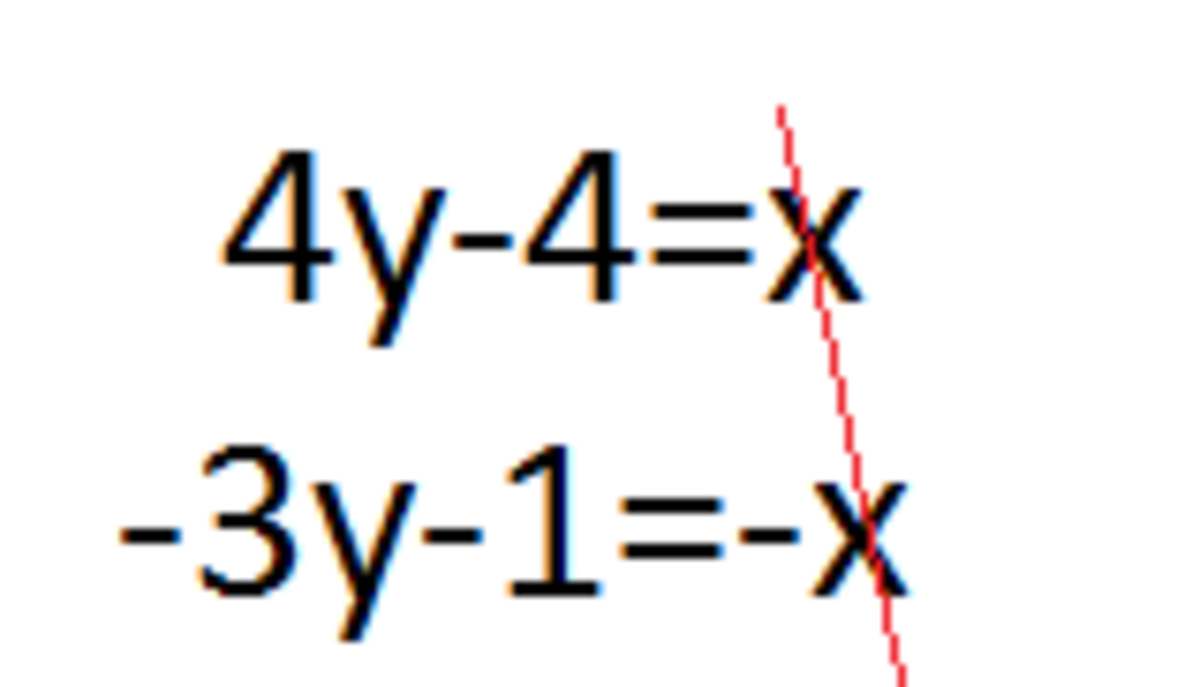
y-5=0 so y=5
As per first constraint,when there are 4 pencils in each jar and one jar is left when all jars are filled. So it's obviously 16 pencils and 5 jars.

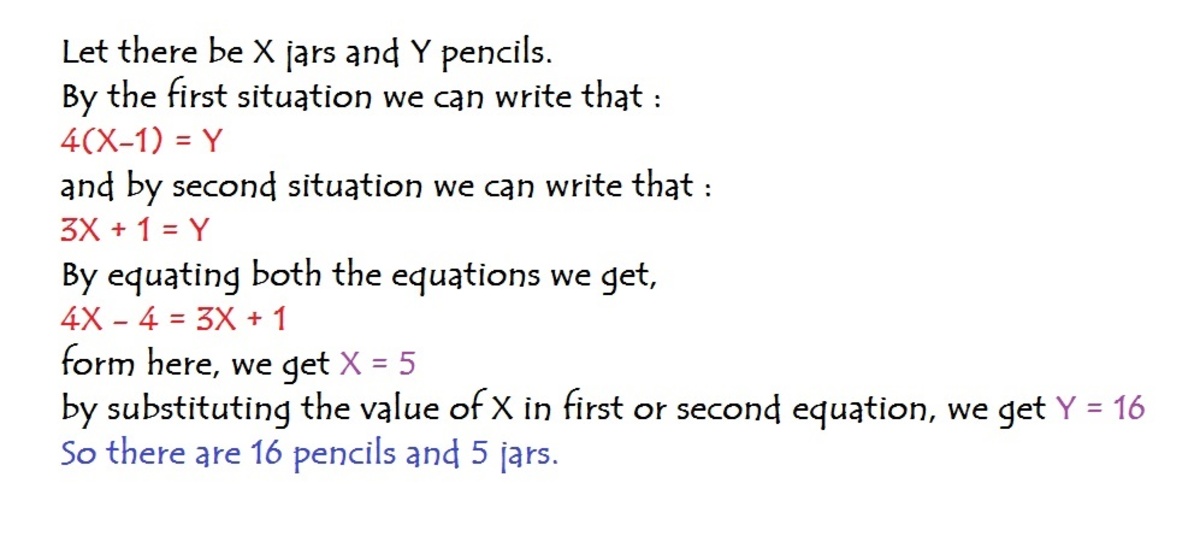
Let there be x pencils and y jars. If 4 pencils are put into each jar there will be one jar left over meaning that 4 pencils into (y-1) jars would divide evenly: 4 x = y − 1
And if 3 pencils go into each jar one pencil is left over so (x-1) pencils divided by 3 goes into y jars: 3 x − 1 = y
These can then be arranged into 2 simultaneous equations by multiplying them by 4 and 3 respectively giving x = 4 y − 4 and x − 1 = 3 y We use substitution to find that y = 5 , x = 1 6 16 pencils and 5 jars! :P