Pendulum clocks

Increasing the temperature will cause the length of the rod to increase. This is due to thermal expansion — the tendency of matter to increase in shape, area, and volume as temperature increases. As the length of the pendulum rod increases so does its period of oscillation. The higher the temperature, the slower the clock will tick.

Since wood expands less than metal, some clocks have wooden pendulums to reduce the impact of thermal expansion.

The time period of pendulum is 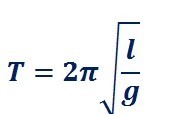from this we can see as the length increases the time period also increases. Initially let the time period be 1 second after the length is increased assume the new time period is increased to 2 second so for covering the same distance pendulum is taking twice the time hence it moves slowly. For further information click here

On increasing temperature LINEAR THERMAL EXPANSION of rod takes place due to which effective length of pendulum increases and as a result time period of oscillation increases

Moving at the same speed, a longer pendulum has more distance to cover than a short one, so it will take longer to cover the distance.

The time period of a pendulum is given by T=2π√(L/g). Where L and g are length of pendulum and gravitational acceleration respectively. If the temperature increases, length of pendulum will also increase because of thermal expansion. And so it's time period will increase. That's why clock will slow down.

Just think what happens when we pull a rope with a weight swinging on it and that is hanging on a tree limb. The pulling movement shortens the hanging rope and the swinging movement becomes faster. The contrary happens when we let some rope loose. That happens also with hanging pinhatas.

The rod as well as the bob that made up the pendulum has been perfectly calibrated for length and weight. Any change or variation in the environment that could result in modifying linear dimension by elevation of temperature or changing weight by effect of gravity will result in specific changes in the length of swing or oscillation, thus changing the length of the unit of time . T = 2π√L/G.

Since T proportional to √l ,so temp.rise will lead to linear thermal expansion i.e. increase in l =>Time period of oscillation increases hence it will cause the clock to lose time.

Because the rod is getting longer, it is getting heavier which causes the rod to move slower.

Time period of pendulum = 2π √l/√g Where l is it's length and g is acceleration due to gravity We can see T^2 is directly proportional to length As length increases time period increases and it runs slower

As the length of the pendulum increases, so does its oscillation time. So because it takes longer to do an oscillation, it will take longer to measure time, thus giving it the appearance of occurring at a slower rate.

as the temperature increase the length of the rod increases and T is prop. to root L . So now the clock's "second" hand moves after time more than one second hence after some time there is fair difference in time between regular clock and our pendulum clock.

By incresing temperature it is obvious that the lenght of pendulum will increase too and so the period.

Clockmakers try to compensate this effect by using for the lentil at the end of pendulum a material with a dilatation coefficient higher than the pendulum ideally with ratio L/D.

Being L the lenght of pendulum and D the diameter of lentil. Now if you allow the lentil moving just upwards freely it will compensate somehow the temperature increase, since center of mass remains at same distance from oscillation point.

Probably you have noticed there is a screw at the botton of pendulum, for a fine adjustment of period and to allow the lentil which rest on it to move upwards , as said above.