Pendulum Frequency
Classical Mechanics
Level
3
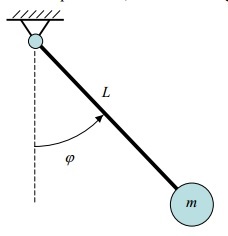How does the frequency of a pendulum change as the amplitude increases?
It increases
It stays the same
It decreases
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Diminishing amplitude is not considered as affecting the frequency but increased of initial angle does.
T ≈ 2π√[L/g{1 + (1/16)θo^2 + (11/3072)θo^4 + (173/737280)θo^6 + ---------}] {Information obtained from the internet.}
For θ = y/ L where Sin θ is replaced by θ as approximation, it effectively increased L and hence increased T. This is because the limit of Sin θ/ θ when θ tends to zero is smaller than 1.
f = 1/ T and therefore frequency decreased.