Pendulum in field

If the string makes an angle $\theta$ with the downward vertical, then we have the equation of motion

$m\ell\dot{\theta}\binom{\cos\theta}{\sin\theta} - m\ell \dot{\theta}^2\binom{\sin\theta}{-\cos\theta} \; = \; -T\binom{\sin\theta}{-\cos\theta} + \binom{F}{-mg}$ where $T$ is the tension in the string, and $F$ is the strength of the wind. Taking the inner product of this equation with $\binom{\cos\theta}{\sin\theta}$ , we see that $m\ell \ddot{\theta} \; = \; F\cos\theta - mg\sin\theta$ This problem has an equilibrium position of $\theta \equiv \alpha$ , where $F\cos\alpha = mg\sin\alpha$ , so $\alpha = \tan^{-1}\tfrac{F}{mg}$ . Now $\begin{aligned} \ddot{\theta} & = \; \frac{\sqrt{F^2 + m^2g^2}}{m \ell}\big(\sin\alpha\cos\theta -\cos\alpha\sin\theta\big) \; = \; -\tfrac{\sqrt{F^2 + m^2g^2}}{m \ell}\sin(\theta-\alpha) \\ \tfrac12\dot{\theta}^2 & = \; \tfrac{\sqrt{F^2+m^2g^2}}{m\ell}\big[\cos(\theta - \alpha) - \cos\alpha\big] \end{aligned}$ so that the particle oscillates between $\theta = 0$ and $\theta = 2\alpha$ . We also note that $T \; = \; \sqrt{F^2 + m^2g^2}\big[3\cos(\theta-\alpha) - 2\cos\theta\big]$ so that $T \ge \sqrt{F^2 + m^2g^2}\cos\alpha = mg > 0$ throughout the motion, and so the string never becomes slack (which, if it happened, would invalidate the model).

Thus the system oscillates about the equilibrium position $\theta = \alpha$ with angular amplitude $\alpha$ . I this case $F=m=g=\ell=10$ , we see that $\alpha =\tan^{-1}\tfrac{1}{10} = \boxed{0.09966865249}$ .

When $F=10000$ (and $m=g=\ell=10$ ), the equilibrium angle is $\tan^{-1}100$ . As $F \to \infty$ , the equilibrium angle tends to $\tfrac12\pi$ .

This is a re-upload, because I made the previous problem with a wrong answer. I entered the maximum value of the angle instead of the amplitude of oscillation.

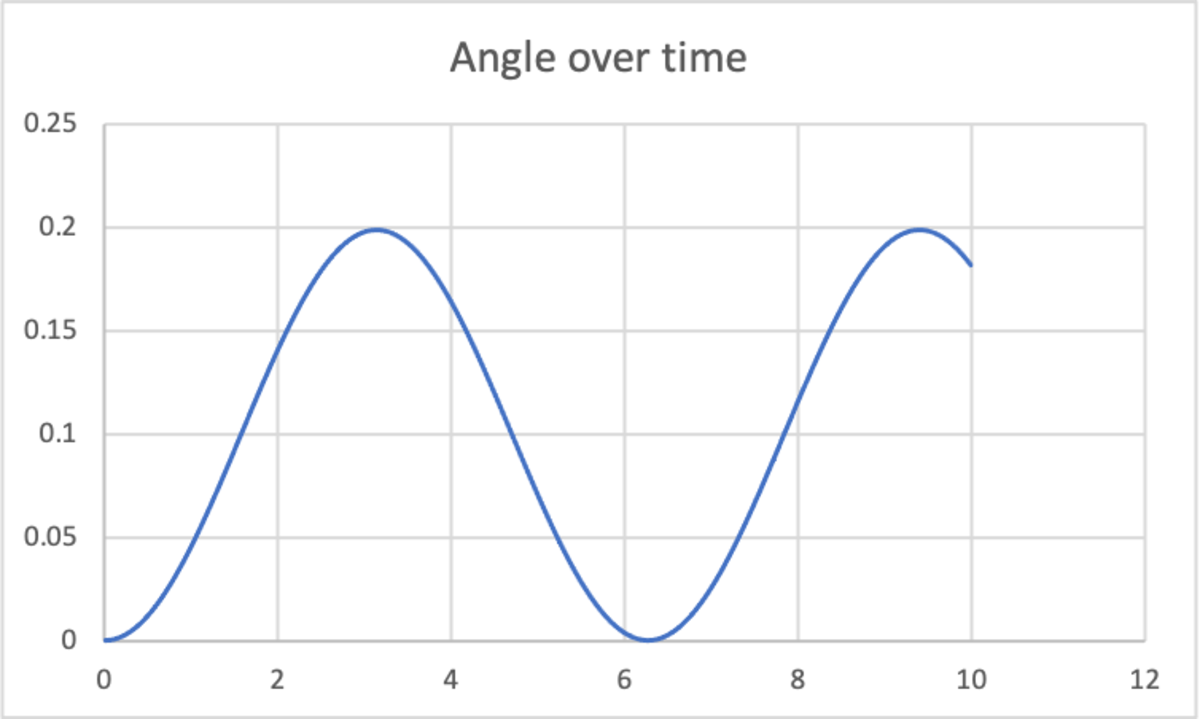
This problem is simple yet interesting, because as the field strength increases greatly, the pendulum exhibits either one of the two behaviours:

• It ragdolls all over the place from $0$ to $\pi$
• However, when it's initial position is at $\displaystyle \frac{\pi}{2}$ , it oscillates with high frequency, but extremely small amplitude as the field strength gets greater. Eventually when the field is infinitely strong, it just stays in equilibrium.

Here's what a graph of the motion at $\displaystyle \theta_{i} = \frac{\pi}{2}$ , and at $\theta_i = 0$

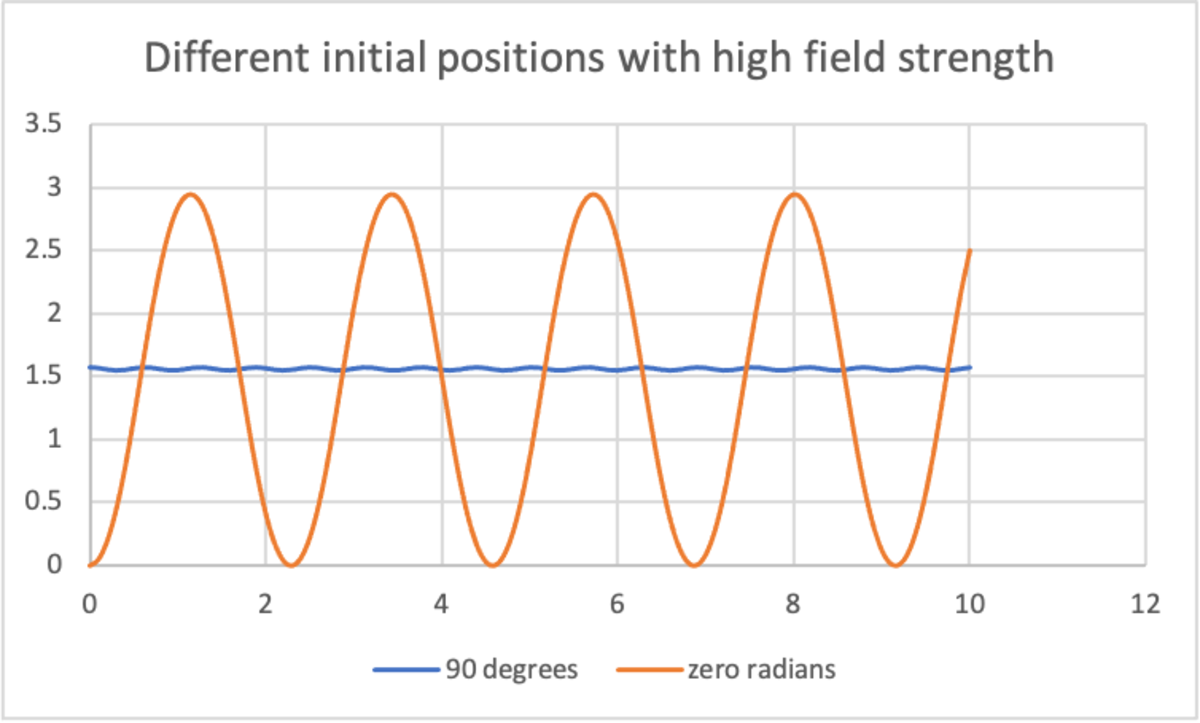
It is easy to see this equilibrium position intuitively because if the bob has any depression or elevation above the $+x$ -axis it is immediately forced back down, so it just stays right at $\displaystyle \frac{\pi}{2}$ when it starts there.

I tried to simulate it, so here's the maths:

The tangential component of gravity is:

$F_g = -mg \sin(\theta)$

Resolving the field's tangential component $\vec{\bold{F}} = f\hat{i} + 0 \hat{j}$ where $f = 10N$ ,

$F_d = f \cos(\theta)$

Newton's 2nd Law:

$ml \ddot{\theta} = -mg \sin(\theta) + f \cos(\theta)$

Solving for $\theta$ and numerically integrating is the last step.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

import math

time = 0
deltaT = 10**-5

l = 10
m = 10
g = 10

theta = math.pi/2
thetaDot = 0

F = 10000
count = 0

while time <= 10:
    if count % 10000 == 0:
        print(theta)

    Fgt = -m*g*math.sin(theta)
    Fdt = F*math.cos(theta)

    totalTangentialForce = Fgt + Fdt 

    thetaDotDot = (Fgt + Fdt)/(m*l)
    thetaDot += thetaDotDot*deltaT
    theta += thetaDot*deltaT



    time += deltaT
    count += 1