Pendulum, pendulum!

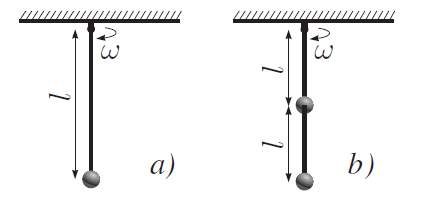
The above figure shows two ball and rod arrangements. In both cases:

• The balls are to be regarded as identical point masses.
• The rods are ideal and identical (mass-less and in-extensible).
• All pivots (one in figure (a) and two in figure (b)) are hinges that can rotate in the vertical plane.
• For (b) the second pivot is between the upper mass and lower rod.

Let ${ \omega }_{ a }$ and ${ \omega }_{ b }$ denote the critical values of angular velocity of rotation of top pivots for cases $a$ and $b$ for which the systems are in stable equilibrium.

Find $\frac{{ \omega }_{ a }}{{ \omega }_{ b }}$

Details: Both systems are in the same room on Earth!