Pendulum Projectile
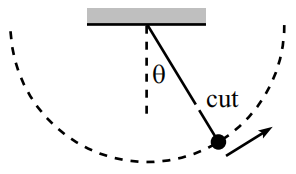
A pendulum is held with its string horizontal and is then released. The mass swings down, and then on its way back up, the string is cut when it makes an angle of with the vertical. Assume that air resistance is negligible.
What should be, so that the mass travels the largest horizontal distance by the time it returns to the height it had when the string was cut?
If the answer can be written as find the value of
The answer is 0.707107.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let's start off with the equations of motion for our ball after it is released from the string. Since we are calculating horizontal distance by the time the ball returns to its launch height, we can let the origin coincide with the point where the ball becomes detached from the string. We then have:
x ( t ) = x 0 + v cos θ t y ( t ) = y 0 + v sin θ t − 2 1 g t 2
Rearranging the first equation for t and plugging it into the second equation, we get:
t = v cos θ x − x 0 ⇒ y ( x ) = y 0 + ( x − x 0 ) tan θ − 2 v 2 cos 2 θ g ( x − x 0 ) 2
Now, to find v , which is the initial velocity of the ball when it is launched, we simply note the ball begin in the horizontal and swung down. The height of the ball when it is located at angle θ will be (from basic trigonometry), L − L cos θ . This means that:
E 0 = m g L E f = m g L ( 1 − cos θ ) + 2 1 m v 2 E 0 = E f ⇒ m g L = m g L ( 1 − cos θ ) + 2 1 m v 2 ⇒ v = 2 g L cos θ
Plugging this into the equation for y ( x ) , we get:
y ( x ) = y 0 + ( x − x 0 ) tan θ − 4 L cos 3 θ ( x − x 0 ) 2
We are interested in the total vertical range of the ball, therefore we set y ( x ) = y 0 , and get:
( x − x 0 ) tan θ − 4 L cos 3 θ ( x − x 0 ) 2 = 0
Let's declutter this expression, we are interested in the change in x after the projectile is launched, therefore we can omit x 0 . Rearranging for a function of x with respect to θ :
x tan θ = 4 L cos 3 θ x 2 ⇒ tan θ = 4 L cos 3 θ x ⇒ x ( θ ) = 4 L tan θ cos 3 θ
We can find the maximum of this function by taking the derivative and setting x ′ ( θ ) = 0 :
d θ d x ( θ ) = d d θ 4 L tan θ cos 3 θ = 4 L ( c o s 3 θ − 2 cos θ sin 2 θ ) ⇒ 4 L ( c o s 3 θ − 2 cos θ sin 2 θ ) = 0 ⇒ c o s 3 θ = 2 cos θ sin 2 θ ⇒ tan θ = 2 1 ⇒ θ = tan − 1 2 1
So this means that our answer is x = 2 1 ≈ 0 . 7 0 7 .