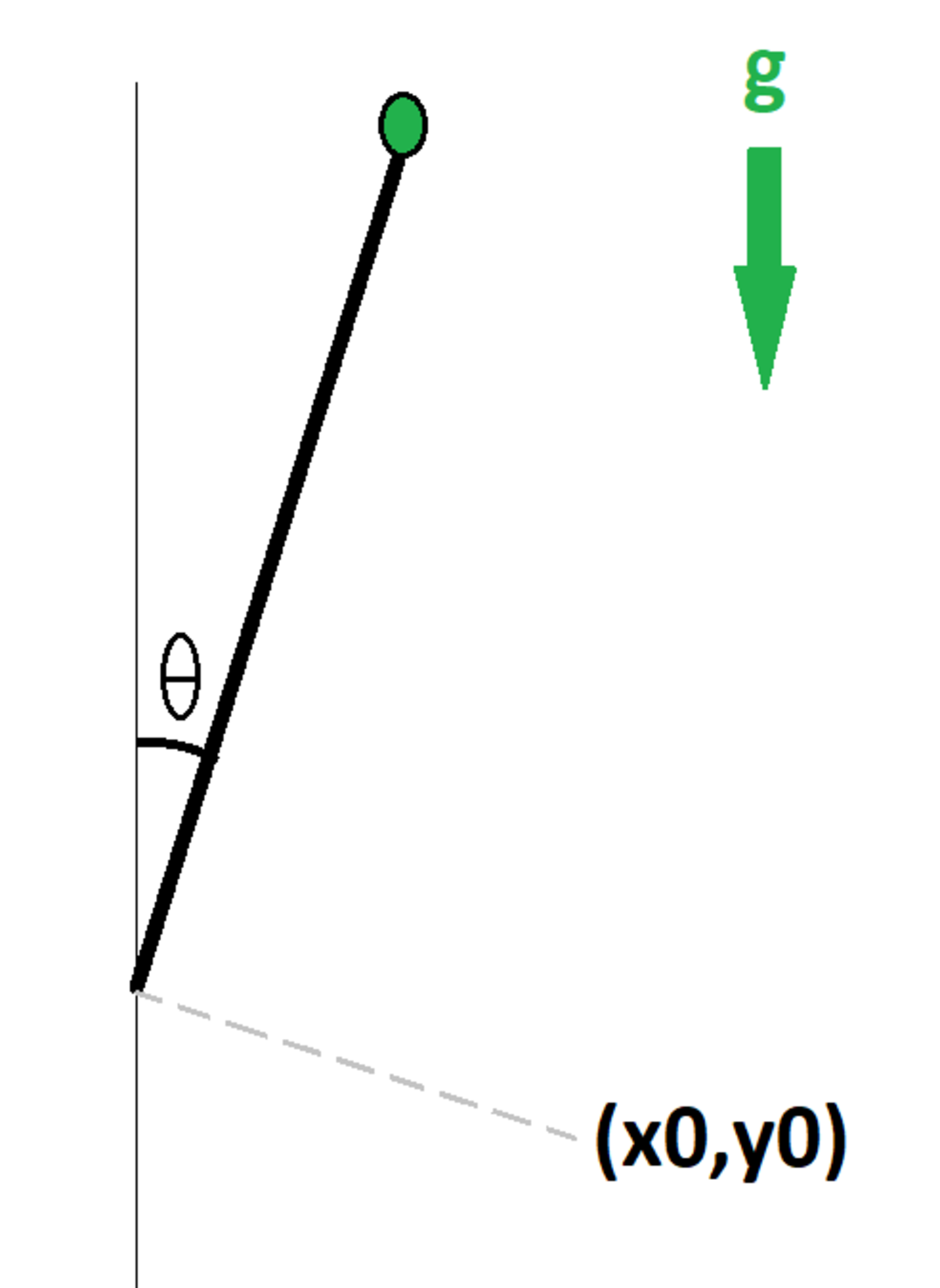
Pendulum with Oscillating Base

The coordinates of the mass are:

$x = L\sin{\theta}$ $y = \frac{\cos(20 \pi t)}{10} + L\cos{\theta}$

The kinetic energy of the mass is (expression shown after simplification:

$\mathcal{T} = \frac{m}{2}(\dot{x}^2 + \dot{y}^2)$ $\mathcal{T} = \frac{m}{2}\left(L^2\dot{\theta}^2 + 4 \pi^2 \sin^2(20 \pi t) + 4 \pi L \dot{\theta}\sin{\theta} \sin(20 \pi t)\right)$ $\implies \mathcal{T} = \frac{\dot{\theta}^2}{2} + 2 \pi^2 \sin^2(20 \pi t) + 2 \pi L \dot{\theta}\sin{\theta} \sin(20 \pi t)$

The potential energy of the mass is:

$\mathcal{V} = mgy$ $\implies \mathcal{V} = \cos(20 \pi t) + 10\cos{\theta}$

The equation of motion can be found by applying Lagrange's equation as follows:

$\frac{d}{dt}\left(\frac{\partial \mathcal{T}}{\partial \dot{\theta}}\right) - \frac{\partial \mathcal{T}}{\partial \theta} + \frac{\partial \mathcal{V}}{\partial \theta}=0$

Crunching out all derivatives yields:

$\boxed{\ddot{\theta} = 10\sin{\theta} - 40 \pi^2 \sin{\theta} \cos(20 \pi t)}$ $\theta(0) = \frac{5 \pi}{180}$ $\dot{\theta}(0) = 0$

I am leaving out the part involving numerical integration.

I will now focus on the bonus part of this problem. The truly remarkable quality of this system is that it is periodic and exhibits stability. One would have expected the pendulum to fall due to gravity from its point of unstable equilibrium. However, the bob of the pendulum oscillates between $\pm 5 ^{\circ}$ about its natural unstable equilibrium. So the sinusoidal driving motion has a stabilising effect on the pendulum's motion.

A plot of angle vs. time is as follows: