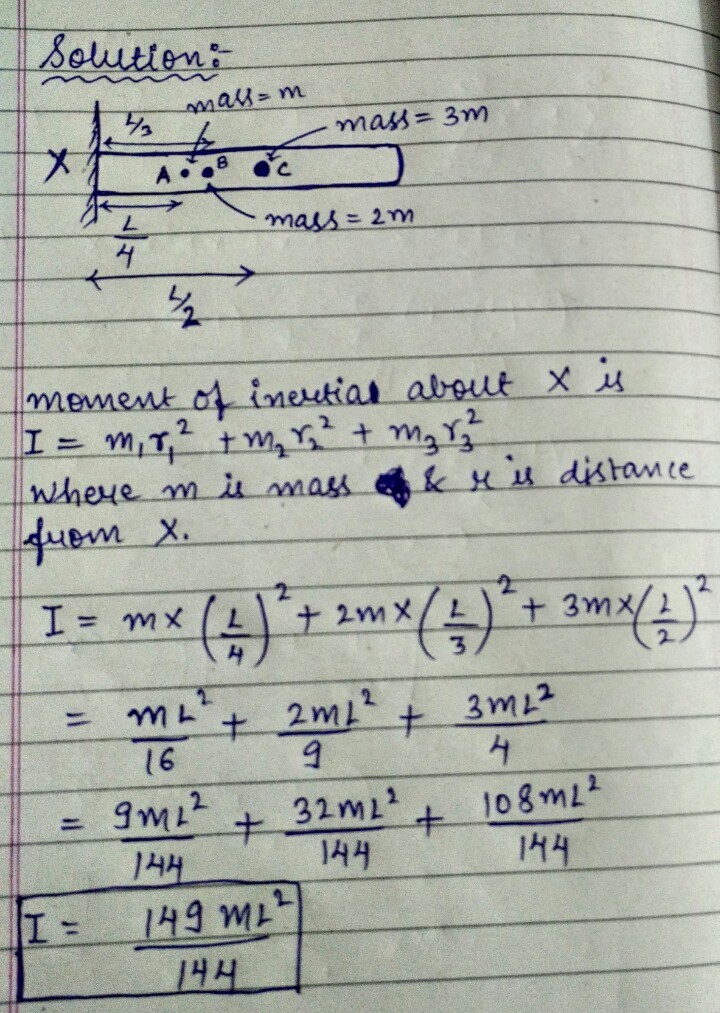Pendulum's moment of inertia

Classical Mechanics Level 3

A nearly massless rod $(XY)$ of length $L$ is pivoted at one end $X$ so that it can swing free as a pendulum. Three masses $A(m),$ $B(2m)$ and $C(3m)$ are attached to it at the distances $\frac{L}{4},$ $\frac{L}{3}$ and $\frac{L}{2},$ respectively, from end $X.$ The rod is held horizontal and then it is released. Find the moment of inertia of the system about the pivoted end.

I = \frac{m{L}^{2}}{144}

I = \frac{151m{L}^{2}}{144}

I = \frac{14m{L}^{2}}{144}

I = \frac{149m{L}^{2}}{144}

1 solution

Raj Rajput
Aug 12, 2015

Pendulum's moment of inertia

1 solution

0 pending reports