Pent-hexagon & Hex-pentagon
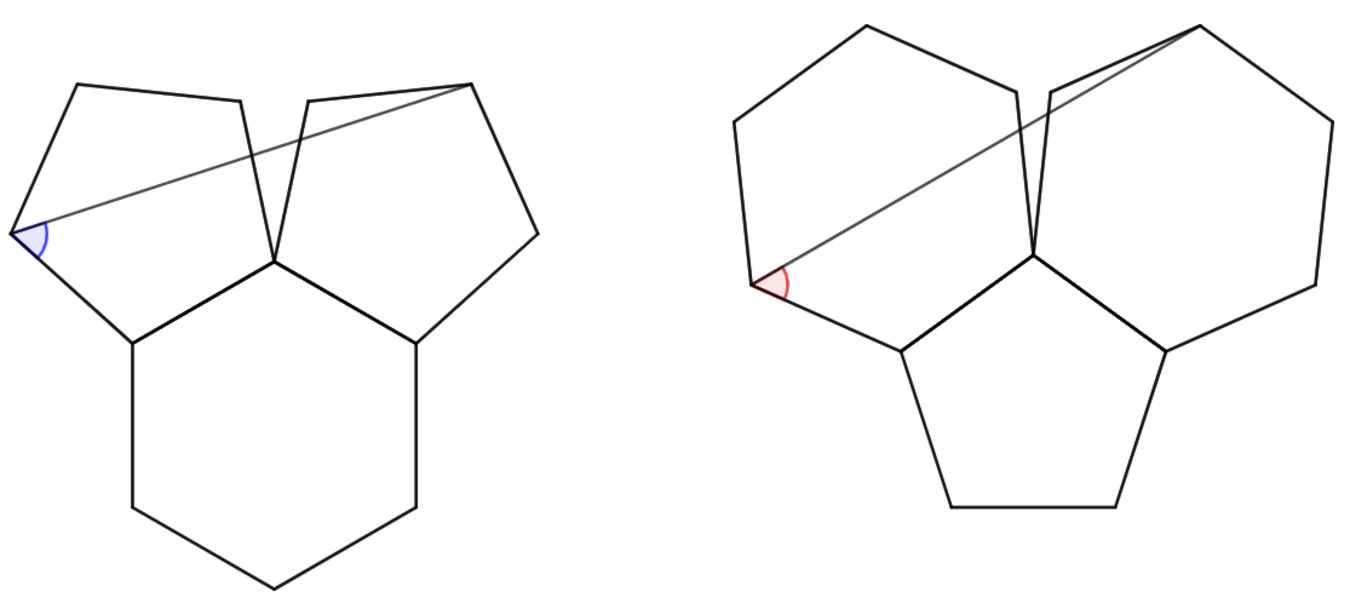
Both diagrams illustrate the combinations of three unit regular polygons. On the left, the hexagon is adjacent to two pentagons touching at a vertex, whereas on the right the pentagon is adjacent to two hexagons also touching at a vertex. The angles are formed as shown above.
Which of the following must be true about the values of the Blue angle and the Red angle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The following is the image by Chew Seong Cheong

For the solution, define the points as follows:
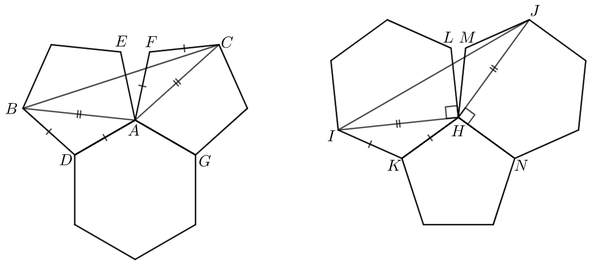
Note that ∠ B A D + ∠ B A E = ∠ F A C + ∠ C A G = 1 0 8 ∘ , which is the interior angle of a regular pentagon. Since △ B A D and △ C A F are both isosceles, ∠ B A D = ∠ G A F = 3 6 ∘ , so ∠ C A G = ∠ B A E = 7 2 ∘ . So
∠ B A C = 3 6 0 ∘ − ( ∠ D A G + ∠ B A D + ∠ C A G ) = 3 6 0 ∘ − ( 1 2 0 ∘ + 1 0 8 ∘ ) = 1 3 2 ∘
Since △ B A C is also isosceles,
∠ C B A = ∠ C A B = 2 1 ( 1 8 0 ∘ − ∠ B A C ) = 2 4 ∘
which tells us that
Blue = ∠ C B A + ∠ A B D = 6 0 ∘
We can follow the similar steps for the pentagon tangent to two hexagons. Angle-chasing, we see that since ∠ L H J = ∠ J H N = 9 0 ∘ and ∠ H I K = ∠ J H M = 3 0 ∘ , then ∠ I H K + ∠ J H N = 1 2 0 ∘ , which also makes up the interior angle of a regular hexagon. Therefore, since
∠ J H I = 3 6 0 ∘ − ( ∠ K H N + 1 2 0 ∘ ) = 1 3 2 ∘ → ∠ J I H = ∠ I J H = 2 4 ∘
It tells us that
Red = ∠ J I H + ∠ H I K = 5 4 ∘
For this problem, Blue > Red
Thanks for posting my image.
Label some of the polygon vertices as seen in the figure.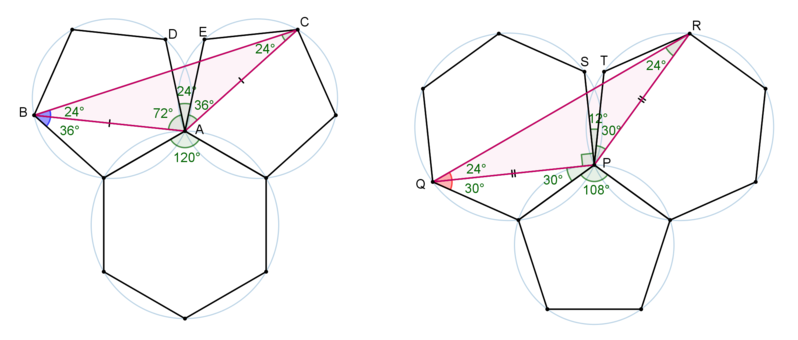
All angles which are inscribed in the circumcircles of the regular polygons have measures which are multiples of 2 1 × 5 3 6 0 ∘ = 3 6 ∘ in the case of the regular pentagons and multiples of 2 1 × 6 3 6 0 ∘ = 3 0 ∘ , in the case of regular hexagons.
Moreover, ∠ D A E = 3 6 0 ∘ − ( 1 2 0 ∘ + 2 × 1 0 8 ∘ ) = 2 4 ∘ and ∠ S P T = 3 6 0 ∘ − ( 1 0 8 ∘ + 2 × 1 2 0 ∘ ) = 1 2 ∘
Furthermore, △ A B C and △ P Q R are isoscele triangles, thus ∠ C B A = 2 1 { 1 8 0 ∘ − ( 7 2 ∘ + 2 4 ∘ + 3 6 ∘ ) } = 2 4 ∘ and ∠ R Q P = 2 1 { 1 8 0 ∘ − ( 9 0 ∘ + 1 2 ∘ + 3 0 ∘ ) } = 2 4 ∘
Combining all the above, we find that B l u e a n g l e = 3 6 ∘ + 2 4 ∘ = 6 0 ∘ a n d R e d a n g l e = 3 0 ∘ + 2 4 ∘ = 5 4 ∘ Hence, B l u e > R e d .