Pentacular
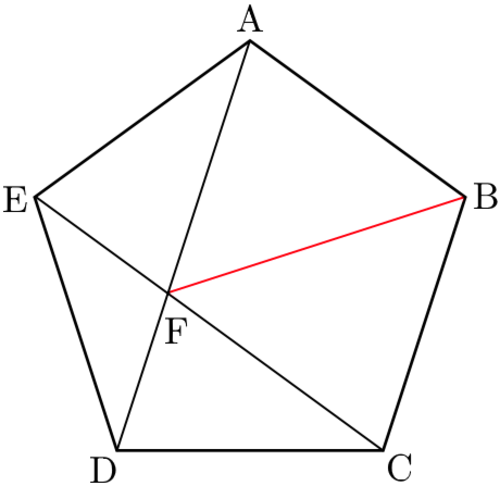 Let the point inside a regular pentagon
where the lines segments
and
intersect be
.
Let the point inside a regular pentagon
where the lines segments
and
intersect be
.
If the pentagon has side length , find the floor of the length of (the line).
Created by Michael Fuller . Popular geometry problems: "Star Stumper" , "Not your average shuriken"
The answer is 58.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
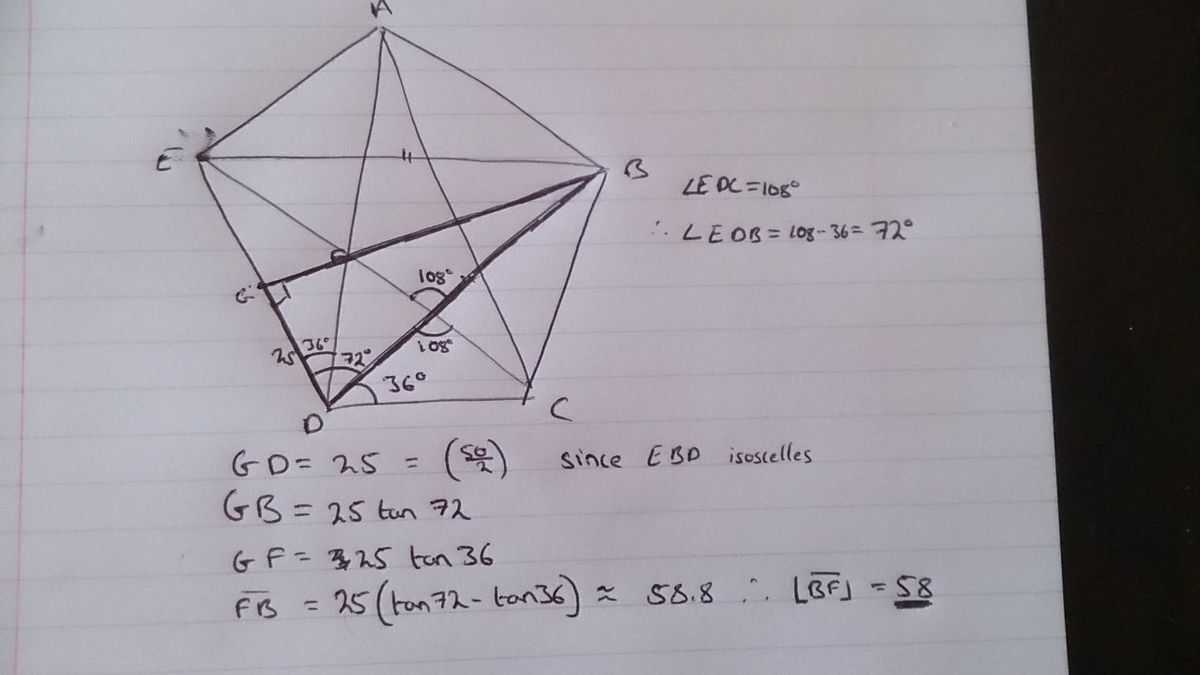
By the law of cosines, B F 2 = 5 0 2 + 5 0 2 − 2 ⋅ 5 0 2 cos ( 5 2 π ) .
That is, B F ≈ 5 8 . 8 , so the answer is 5 8 .