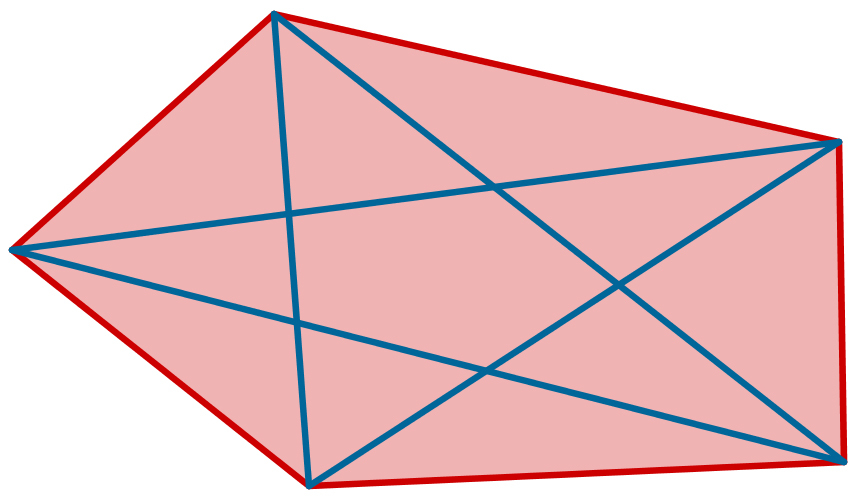
Pentagon
Let denote the perimeter of a convex pentagon, and let denote the sum of diagonals of this same pentagon.
Is it true that for any convex pentagon, is fulfilled?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
All triangles must not have one side that is longer than the sum of the other two. If we look at every side of the large pentagon individually, we can see that the triangle it forms with the two closest segments of the diagonals must have the segments from the diagonals being longer than the side from the pentagon. Since none of these bits will overlap we can say that for every side of the pentagon there is more from the diagonals, so d > p. Then we look at the triangles formed by adjacent pairs of sides from the pentagon and the diagonal between them. We can see that for each of these pairs the perimeter from the pentagons will be more than the perimeter from the diagonal. If we look at all these pairs we can see that 2p > d.