Pentagon and a circle

Suppose yes. Then we can use the figure below.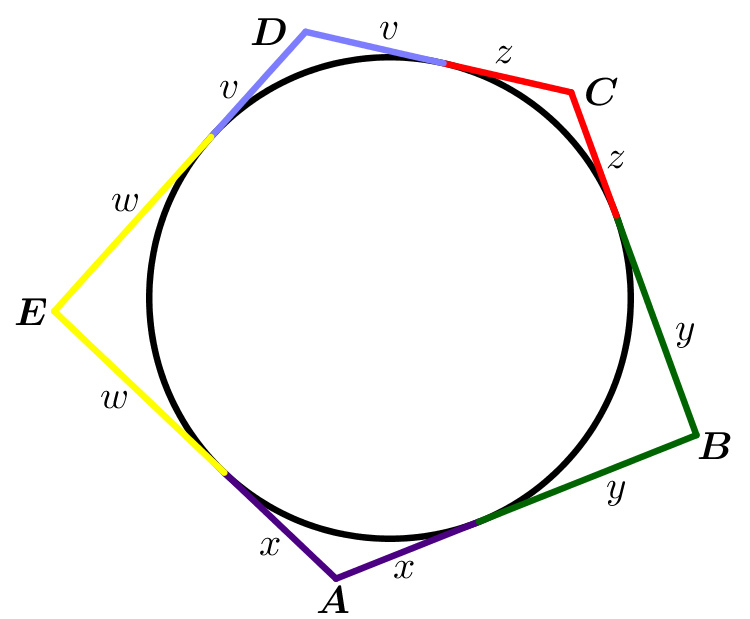

$x+y+z+v+w=\dfrac{(x+y)+(y+z)+(z+v)+(v+w)+(w+x)}{2}=\dfrac{1+2+3+4+6}{2}=8$ Let's assume, that the $AB$ side's length is $6$ . Then $(x+y)=6$ , so $z+v+w=8-6=2$ . From that both of the $CD=z+v$ and the $DE=v+w$ side's lenght is smaller, than $2$ , but from the $1, 2, 3, 4, 6$ numbers, only one is smaller then $2$ , which is a contradiction.

So the answer is: not possible.

Each side of Pentagon is a sum of two tangent lengths with each of these lengths also a tangent length in adjacent side. Let us say that the side length 6 is a sum of two tangents of lengths x and (6-x).
Since these lengths have also to be carved out of the adjacent sides, x should be more than 2, otherwise the tangent length of (6-x) will not be possible on adjacent side. With x=>2, the two sides adjacent to 6 can only be 3 and 4. The side 3 will consist of two tangents of lengths x and
(3-x) and the side of length 4 will comprise two tangents of lengths (6-x) and 4 - (6-x) = (x - 2).
The remaining two sides are of lengths (1,2) or (2,1). The tangents of lengths (3-x) and (x-2) will have to be carved out of sides (1,2) or (2,1) and the balance lengths left on these sides should be equal, being the final tangent.
So, we have,
1 - (3-x) = 2 - (x-2), => x = 3, Or
2 - (3-x) = 1 - (x-2), => x = 2,
If x = 3, the tangent length (3-x) becomes 0 and the sides 3 and 1 are joined in a straight line and it is not a Pentagon but a quadrilateral. If x = 2, the tangent (x-2) = 0, and sides 4 and 1 get joined in a straight line and it no longer remains a Pentagon.
Hence the Pentagon with given sides would not be possible.