Pentagon in a Square???Sounds Strange!!!

Probability Level 5

Aaron takes a square sheet of paper with one corner labelled as A A . Point P P is chosen at random inside the square and Aaron folds the paper so that A A and P P coincide. He cuts the sheet along the crease and discards the piece containing A A . Let p p be the probability that the remaining piece is a pentagon. Find the integer nearest to 100 p 100p .


The answer is 57.

Yash Singhal by Yash Singhal , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

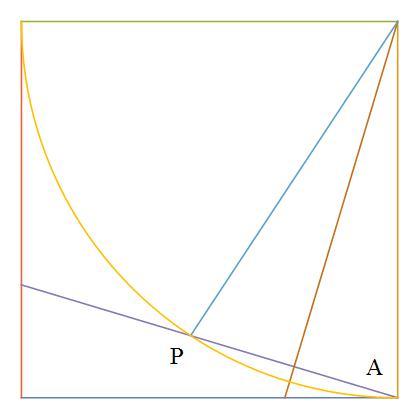
EDIT : point A is the bottom right vertex of square \text{EDIT : point A is the bottom right vertex of square}

It is not very hard to think that locus of limiting position of the required point P \text{P} is indeed the boundry of shaded region , with the knowledge of this fact the problem becomes almost trivial .

We want all points that lie inside \color{#20A900}{\text{inside}} of the boundry of the shaded region ,

So required probability \text{required probability} = area of shaded region total area of square \dfrac{\text{area of shaded region}}{\text{total area of square}}

Take the side length 1 1 {as the side length doesn't effect probability} and on simple calculations you will find that the area of shaded region is π 2 − 1 \dfrac{\pi}{2} -1 which would be numerically equal to the probability as area of square equals 1 1 .

Thus required probability is 0.570796 \boxed{0.570796}

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Michael Mendrin
Jun 12, 2015

To buttress Siddarth's solution, check this graphic out to see how those arcs are indeed circular

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Thanks sir, I was wondering if there was any software/app that you used to draw that , would you mind telling me?

Siddharth Bhatnagar - 6 years ago

Log in to reply

An old mathematica software. Still works.

Michael Mendrin - 6 years ago

You can also use geogebra, the software is free and can easily be downloaded.

Will Wombell - 5 years, 9 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...