pentagon inscribed in triangle
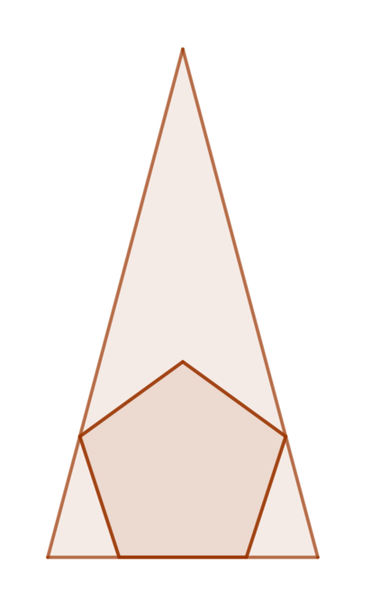 The figure shows a regular pentagon inscribed in an isosceles triangle. One side of the pentagon rests on the base of the triangle, while two pentagon vertices touch the legs of the triangle.
The figure shows a regular pentagon inscribed in an isosceles triangle. One side of the pentagon rests on the base of the triangle, while two pentagon vertices touch the legs of the triangle.
If the largest ratio of the pentagon area to the triangle area is given by , where and are integers and is square-free, submit .
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the radius of the regular pentagon be 1 . This means that we have fixed the area of the pentagon to A p = 2 5 sin 7 2 ∘ = 5 sin 3 6 ∘ cos 3 6 ∘ ; and we are looking for the smallest inscribing isosceles triangle.
The area of the triangle is A △ = A C ⋅ B C . Let the apex angle of the isosceles triangle be θ . Then
A C = A D + D C = D E ⋅ cot 2 θ + E F ⋅ cos 1 8 ∘ = cos 1 8 ∘ cot 2 θ + 2 sin 3 6 ∘ cos 1 8 ∘ = cos 1 8 ∘ ( cot 2 θ + 2 sin 3 6 ∘ )
And B C = A C ⋅ tan 2 θ . Therefore,
A △ = cos 2 1 8 ∘ ( cot 2 θ + 2 sin 3 6 ∘ ) 2 tan 2 θ = cos 2 1 8 ∘ ( 1 + 2 sin 3 6 ∘ tan 2 θ ) ( cot 2 θ + 2 sin 3 6 ∘ ) = cos 2 1 8 ∘ ( cot 2 θ + 4 sin 3 6 ∘ + 4 sin 2 3 6 ∘ tan 2 θ ) ≥ cos 2 1 8 ∘ ( 4 sin 3 6 ∘ + 4 sin 3 6 ∘ ) By AM-GM inequality Equality occurs when cot 2 θ = 2 sin 3 6 ∘
⟹ min ( A △ ) = 8 cos 2 1 8 ∘ sin 3 6 ∘
Then we have:
min ( A △ ) A p = 8 cos 2 1 8 ∘ sin 3 6 ∘ 5 sin 3 6 ∘ cos 3 6 ∘ = 4 cos 3 6 ∘ + 4 5 cos 3 6 ∘ = 4 ( 5 + 1 + 4 ) 5 ( 5 + 1 ) = 4 ( 5 + 5 ) 5 ( 5 + 1 ) = 4 5 ( 5 + 1 ) 5 ( 5 + 1 ) = 4 5 Note that cos 3 6 ∘ = 4 5 + 1
Therefore a + b = 5 + 4 = 9 .
Reference: AM-GM inequality