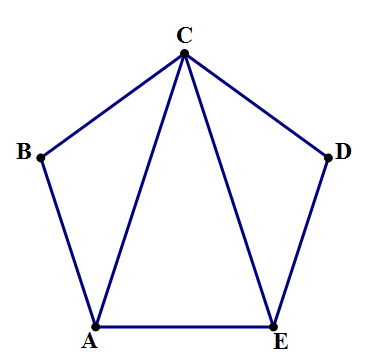
Pentagon Problem
Given that ABCDE is a regular pentagon, what is the measure of angle ACE in degrees?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
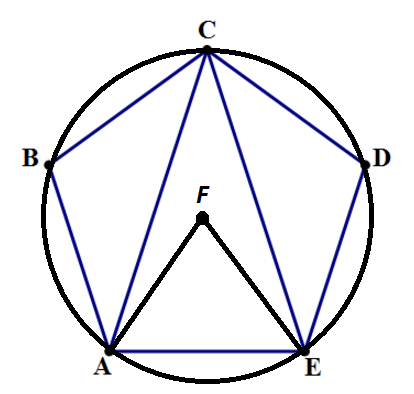
Given that ABCDE is a regular pentagon. The points A, B, C, D, E are on circle with center F (See figure above).
Therefore, ∠ A C E = 2 ∠ A F E where ∠ A F E = 7 2 ∘ (because ∠ A F E is the central angle of the regular pentagon ABCDE).
So ∠ A C E = 2 7 2 ∘ = 3 6 ∘ .
First of all, all the angles in any n-sided polygon add up to ( n − 2 ) × 1 8 0 ° . For any pentagon, that would be 3 × 1 8 0 ° = 5 4 0 ° . For a regular pentagon, the five angles are equal, so each one is 540/5 = 108°.
Now, look at isosceles triangle ABC, with an angle of 108° at B. The other two angles are equal: call each x . 1 0 8 + x + x = 1 8 0 , which leads to x = 3 6 ° .
So, ∠BAC = 36° and ∠ECD = 36°, which means that ∠ACE = 36°