Pentagon to Decagon
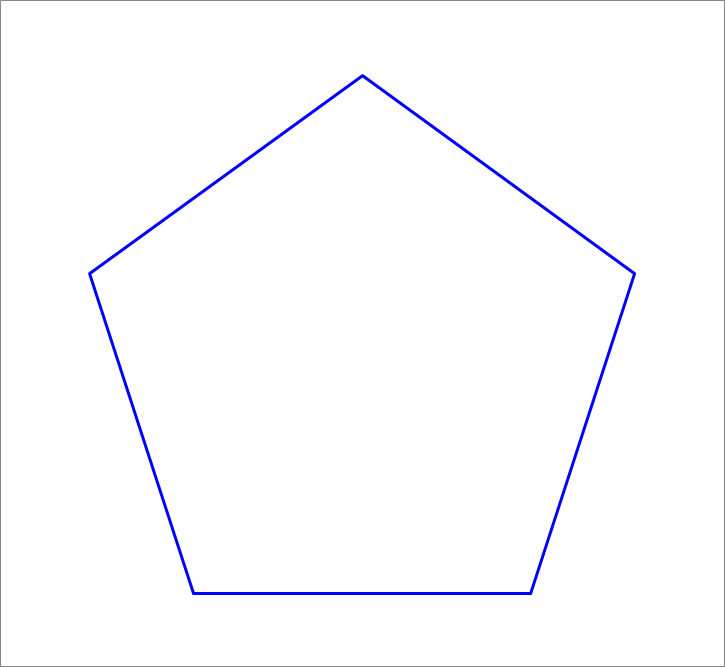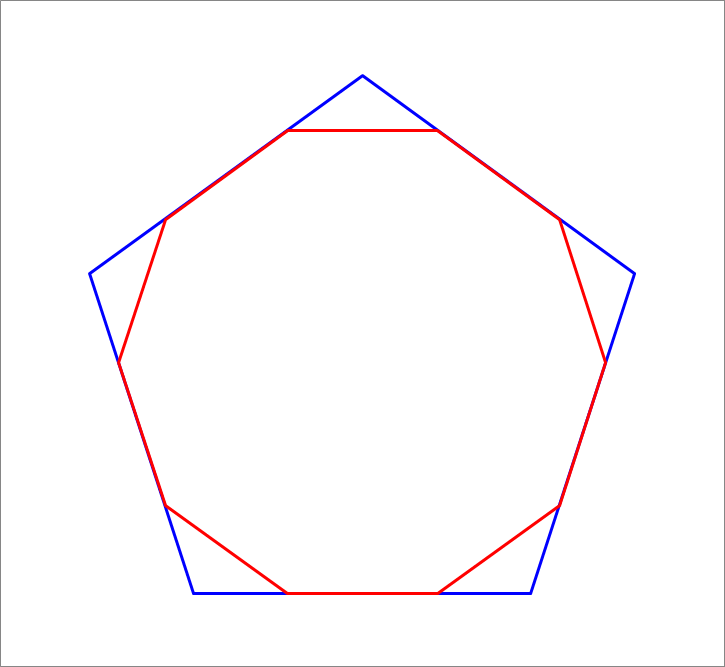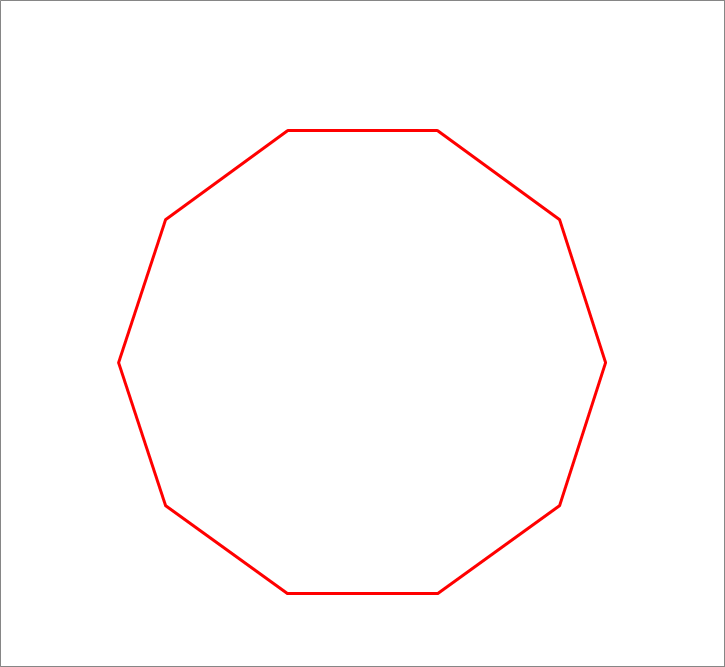
The attached animation shows how to transform a given regular pentagon to a regular decagon (10 sides), namely by cutting the 5 corners out at specific distances from each vertex. If the side length of the original pentagon is 100, what is the side length of the resulting decagon ? Round your answer to 2 decimal places.
The answer is 44.72.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
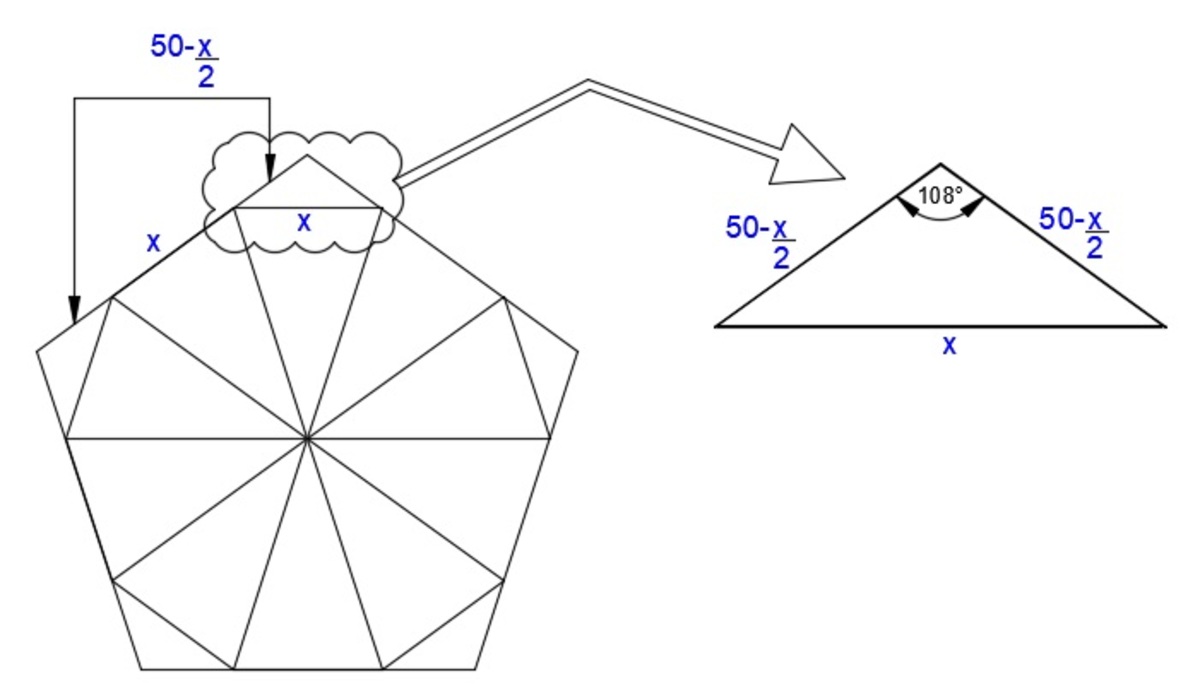 By law of cosines,
By law of cosines,
x 2 = ( 5 0 − 2 x ) 2 + ( 5 0 − 2 x ) 2 − 2 ( 5 0 − 2 x ) ( 5 0 − 2 x ) ( cos 1 0 8 ∘ )
x 2 = 2 5 0 0 − 5 0 x + 4 x 2 + 2 5 0 0 − 5 0 x + 4 x 2 − 2 cos 1 0 8 ∘ ( 2 5 0 0 − 5 0 x + 4 x 2 )
0 . 3 4 5 5 x 2 + 1 3 0 . 9 x − 6 5 4 5 . 0 8 = 0
Use the quadratic formula, to solve for x , we have
x 2 ( 0 . 3 4 5 5 ) − 1 3 0 . 9 ± ( − 1 3 0 . 9 ) 2 − 4 ( 0 . 3 4 5 5 ) ( − 6 5 4 5 . 0 8 )
x = − 1 8 9 . 4 4 ± 1 2 3 . 1 6
get the positive value
x ≈ 4 4 . 7 2
cos 1 0 8 is radian, cos 1 0 8 ∘ is degree.
Let x be the distance between a vertex of the decagon and the closest vertex of the pentagon, and y be the side length of the decagon, as shown below on the left.
From the right triangle shown on the right, we get 2 y = x cos 3 6 ∘ , i.e. y = 2 x cos 3 6 ∘ . Then looking at the side length of the pentagon,
2 x + y 2 x + 2 x cos 3 6 ∘ x ( 1 + cos 3 6 ∘ ) x = 1 0 0 = 1 0 0 = 5 0 = 1 + cos 3 6 ∘ 5 0
and then the side length of the decagon is
y = 2 x cos 3 6 ∘ = 1 + cos 3 6 ∘ 1 0 0 cos 3 6 ∘ ≈ 4 4 . 7 2