Pentagonal Kenmotu
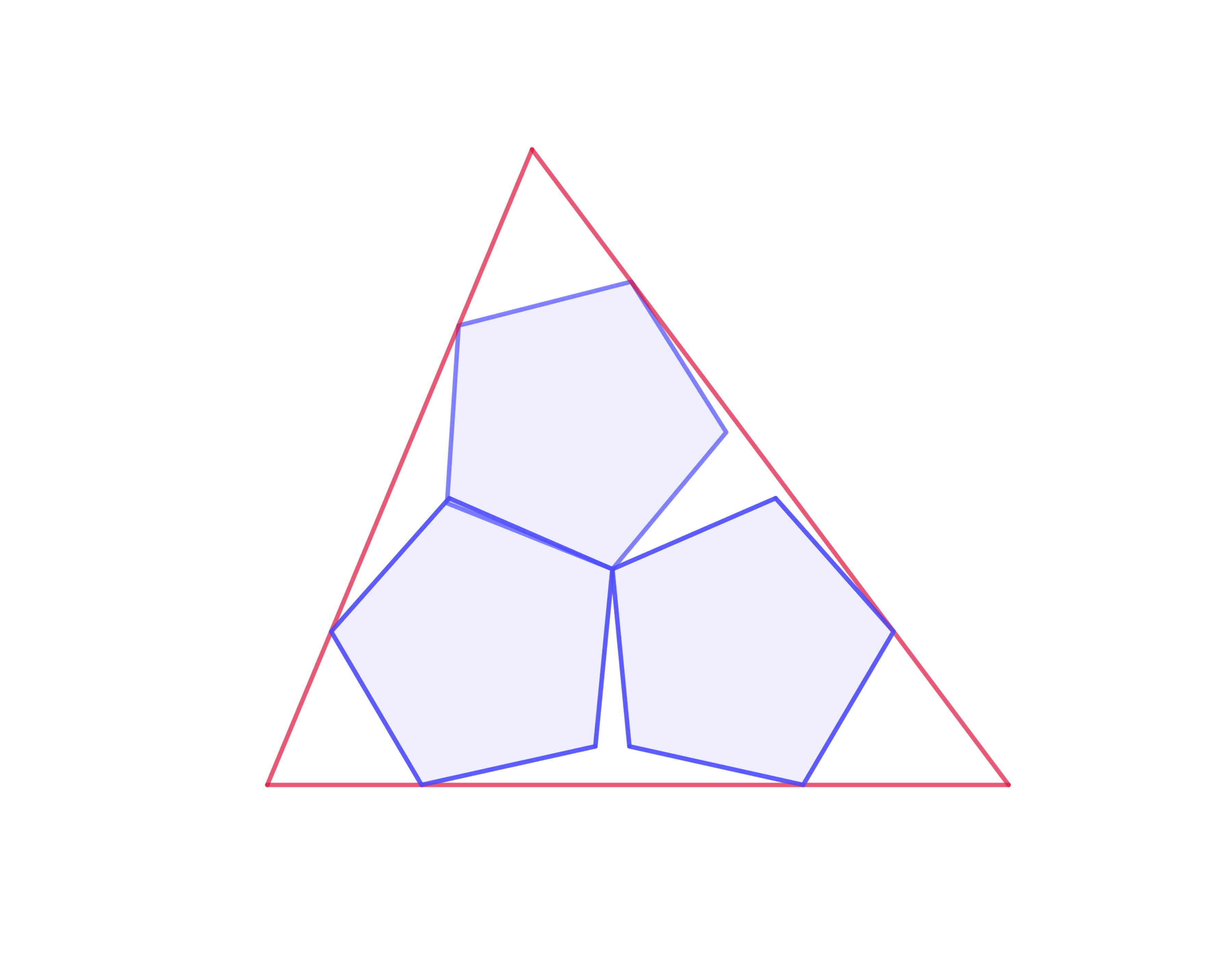
As shown in the figure, three congruent regular pentagons, sharing a common vertex, are inscribed in △ A B C with the other two vertices of each pentagon touching the sides of △ A B C of lengths 1 3 , 1 4 , and 1 5 .
If the side length of the pentagon is b 2 5 + 5 + c a , where a , b and c are coprime positive integers, submit a + b + c .
Similar Problems:
The answer is 3193.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Very elegant!
 Figure 1
Let’s give a solution similar to the one used in
Triangular Kenmotu
and in
A Squared Triangle
. The original idea of this approach, where we use only tools of elementary geometry, belongs to @Chew-Seong Cheong.
Figure 1
Let’s give a solution similar to the one used in
Triangular Kenmotu
and in
A Squared Triangle
. The original idea of this approach, where we use only tools of elementary geometry, belongs to @Chew-Seong Cheong.
Let ∠ L X M = α , ∠ K X J = β , and ∠ O X P = γ (figure 1). We note that △ X P O is isosceles, thus, ∠ X P O = 9 0 ∘ − 2 γ , hence, ∠ M P B = 1 8 0 ∘ − ( 9 0 ∘ − 2 γ ) − 7 2 ∘ = 2 γ + 1 8 ∘ , thus, ∠ L M X = ∠ L M P − 7 2 ∘ = ( 2 γ + 1 8 ∘ + B ) − 7 2 ∘ = B + 2 γ − 5 4 ∘ .
In isosceles △ X M L , ∠ L X M + 2 ⋅ ∠ L M X = 1 8 0 ∘ ⇒ a + 2 ( B + 2 γ − 5 4 ∘ ) = 1 8 0 ∘ ⇒ a = 2 8 8 ∘ − 2 B − γ . Similarly, β = 2 8 8 ∘ − 2 A − γ .
Moreover,
α + β + γ + 3 ⋅ 3 6 ∘ α + β + γ ( 2 8 8 ∘ − 2 B − γ ) + ( 2 8 8 ∘ − 2 A − γ ) + γ = 3 6 0 ∘ = 2 5 2 ∘ = 2 5 2 ∘ ⇒ γ = 3 2 4 ∘ − 2 ( A + B ) = 3 2 4 ∘ − 2 ( 1 8 0 ∘ − C ) = 2 C − 3 6 ∘ ⇒ 2 γ = C − 1 8 ∘ Similarly, 2 α = A − 1 8 ∘ and 2 β = B − 1 8 ∘ .
Using Heron’s formula we find the area of △ A B C : [ A B C ] = 8 4 .
Let the diagonal length of the pentagons be d and the altitudes from X to B C , C A and A B be h a , h b , and h c respectively. Then the area of △ A B C is also given by: 2 h a ⋅ B C + h b ⋅ C A + h c ⋅ A B 2 1 ( 1 5 d cos 2 α + 1 3 d cos 2 β + 1 4 d cos 2 γ ) = [ A B C ] = 8 4 ( 1 )
In order to calculate
cos
2
α
,
cos
2
β
and
cos
2
γ
, we first find the sines and cosines of the angles of
△
A
B
C
.
We notice that
△
A
B
C
is a compound of a
5
-
1
2
-
1
3
and a
9
-
1
2
-
1
5
right-angled triangles (figure 2).
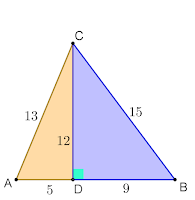 Figure 2
Figure 2
Thus, it is easy to find that
cos
A
=
1
3
5
,
sin
A
=
1
3
1
2
,
cos
B
=
1
5
9
,
sin
A
=
1
5
1
2
.
By sine law,
1
4
sin
C
=
1
5
sin
A
⇒
sin
C
=
1
4
1
4
⋅
1
3
1
2
⇒
sin
C
=
6
5
5
6
.
cos
C
=
1
−
sin
2
C
=
1
−
(
6
5
5
6
)
2
⇒
cos
C
=
6
5
3
3
Combining the results obtained, we get
cos 2 α = cos ( A − 1 8 ∘ ) = cos A ⋅ cos 1 8 ∘ + sin A ⋅ sin 1 8 ∘ = 1 3 5 ⋅ 4 1 0 + 2 5 + 1 3 1 2 ⋅ 4 5 − 1 Similarly, cos 2 β = cos ( B − 1 8 ∘ ) = 1 5 9 ⋅ 4 1 0 + 2 5 + 1 5 1 2 ⋅ 4 5 − 1 cos 2 γ = cos ( C − 1 8 ∘ ) = 6 5 3 3 ⋅ 4 1 0 + 2 5 + 6 5 5 6 ⋅ 4 5 − 1
Finally, after substitutions and simplification,
(
1
)
⇒
d
[
6
5
1
6
8
⋅
1
0
+
2
5
+
1
3
5
9
⋅
(
5
−
1
)
]
=
8
4
which solves to
d
=
2
9
5
(
5
−
1
)
+
1
6
8
2
(
5
+
5
)
5
4
6
0
In a regular pentagon of side
s
and diagonal
d
it holds
s
d
=
φ
, where
φ
=
2
1
+
5
is the golden ratio. Hence,
s
=
φ
d
⇒
s
=
2
9
5
(
5
−
1
)
+
1
6
8
2
(
5
+
5
)
5
4
6
0
⋅
1
+
5
2
which simplifies to
s
=
1
6
8
5
+
2
5
+
2
9
5
2
7
3
0
For the answer,
a
+
b
+
c
=
2
7
3
0
+
1
6
8
+
2
9
5
=
3
1
9
3
.
Note: In the figure we see that two of the pentagons do overlap, unlike the case of equilateral triangles and squares inscribed in the same triangle
△
A
B
C
. Indeed,
β
=
2
c
o
s
−
1
(
1
5
9
⋅
4
1
0
+
2
5
+
1
5
1
2
⋅
4
5
−
1
)
≈
7
0
.
2
6
∘
<
2
⋅
3
6
∘
.
Thank you again for the detailed solution.
Log in to reply
You wellcome. It's a nice problem. I wonder if we can generalise it for n-gons with an odd number of sides...
Log in to reply
I think in general the same pattern works for any set of similar isosceles triangles on the sides and then congruent ones with the common vertex. For pentagon in this case it is equivalent to 72 x 72 x 36 triangles. For square it is 45 x 45 x 90 triangles. For larger n, n-gons will start to overlap quickly. This will tie in to the Kiepert Hyperbola.
The common vertex is the triangle center X(3396) which is isogonal conjugate of X(1139) - OUTER PENTAGON POINT. In plain terms, the point can be constructed by creating regular pentagons outward on triangle sides and connecting outermost points to the opposite vertices of the triangle. This will produce point X(1139). Then the connecting lines need to be reflected on angle bisectors of corresponding angles. This will produce point X(3396). The Trilinear Coordinates are equivalent to cos ( A − π / 1 0 ) : cos ( B − π / 1 0 ) : cos ( C − π / 1 0 )
The numbers can be obtained by using formulae for Exact Trilinear Coordinates . a=2730 , b= 168,c= 295.
Generalization: After trying three Kenmoto problems involving equilateral triangle , square , and regular pentagon, I notice that we can reduce square and pentagon Kenmoto problems to an isosceles triangle Kenmoto problem, where the isosceles triangle is formed by joining the shared center vertex of the regular polygon to the two vertices touching the side of the inscribing triangle. Then the length of the leg of the isosceles triangle is given by:
r = a cos 2 α + b cos 2 β + c cos 2 γ 2 Δ where ⎩ ⎪ ⎨ ⎪ ⎧ α = 2 A − θ β = 2 B − θ γ = 2 C − θ
where Δ is the area of the inscribing triangle, a , b , and c and α , β , and γ are the side lengths of the inscribing triangle and the angles between the isosceles triangles opposite vertices A , B , and C respectively, and θ is the apex angle of the isosceles triangles. For equilateral triangle θ 3 = 6 0 ∘ , for square θ 4 = 9 0 ∘ , and regular pentagon θ 5 = 3 6 ∘ . Putting in the values, we get
r 3 r 4 r 5 = 1 8 1 6 1 9 5 0 − 3 5 2 8 0 3 = 4 6 3 1 3 6 5 2 = 2 9 5 ( 5 − 1 ) + 1 6 8 2 ( 5 + 5 ) 5 4 6 0
And the side length of the pentagon s = 2 cos 3 6 ∘ r 5 = 1 6 8 5 + 2 5 = 2 9 5 2 7 3 0 . Therefore the required answer 2 7 3 0 + 1 6 8 + 2 9 5 = 3 1 9 5 .