Pentagonal Numbers - Finding The Formula

$f(n+1)-f(n)=3n+1$

Put n+1=N

$f(N)-f(N-1)=3N-2$

$f(N-1)-f(N-2)=3(N-1)-2$

.

.

.

$f(2)-f(1)=3 \times 2-2$

Take the sum of all equations

$f(N)-f(N-1)+f(N-1)-f(N-2)+......-f(2)+f(2)-f(1)=3\sum_{i=2}^{N}N - 2(N-1)$

$f(N)-1=3( \frac {N(N+1)} {2}-1)-2N+2$

$f(N)=[3(N^2+N-2)-4N+6]/2$

$= \frac {3N^2+3N-4N} {2}$

$= \frac {3N^2-N} {2}$

$= \frac {N(3N-1)} {2}$

Change of variables:

$f(n)= \frac {(3n-1)(n)} {2}$

We test the given functions in the options. Firstly, because we want $f(1) = 1$ , we only have to consider the options of $f(n) = \frac{ n(n+1) } {2}$ or $f(n) = \frac{ (3n-1) n } { 2}$ .

Next, we check the other condition. For $f(n) = \frac{ n(n+1) } { 2}$ , we have $f(n+1) - f(n) = \frac{ (n+1) (n+2) - n (n+1) } { 2} = n+1$ , which doesn't satisfy the condition.

For $f(n) = \frac{ n(3n-1) } { 2}$ , we have $f(n+1) - f(n) = \frac{ (n+1) (3n+2) - n (3n-1) } { 2} = 3n +1$ , hence this is the answer.

$f(1)=1$

$f(2)=1+4=5$

$f(3)=1+4+7=12$

$...$

$f(n)=1+4+7+...+(3n-2)=\frac{n (1+3n-2)}{2}=\boxed{\frac{3n^{2}-n}{2}}$

$Use\quad the\quad method\quad of\quad finite\quad differences\quad to\quad find\quad the\quad polynomial\quad for\\ any\quad integer\quad sequences\quad that\quad can\quad be\quad expressed\quad by\quad a\quad polynomial.\\ 1,5,12,22,35\\ 4,7,10,12\\ 3,3,3\\ 0,0\\ Let\quad a0=1,\quad a1=4,\quad a2=3,\quad a3=0,...,the\quad first\quad integer\quad in\quad successive\quad rows.\\ Then\quad the\quad polynomial\quad that\quad will\quad give\quad the\quad nth\quad term\quad is:\\ a0\frac { (n-1)! }{ 0!(n-1-0)! } +a1\frac { (n-1)! }{ 1!(n-1-1)! } +a2\frac { (n-1)! }{ 2!(n-1-2)! } +a3\frac { (n-1)! }{ 3!(n-1-3)! } +...\\ which\quad simplifies\quad to\quad \frac { 1 }{ 2 } n(3n-1)\quad for\quad this\quad integer\quad sequence\quad given.\\ \\ \\ \\$

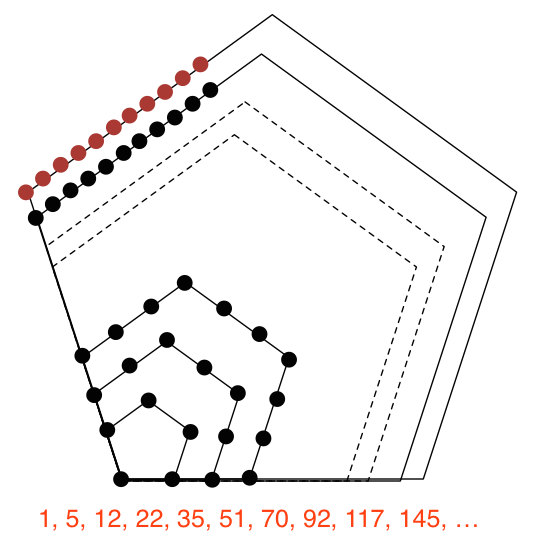
the pentagonal nos.are as follows:

1
1+4=5
1+4+7=12
1+4+7+10=22
1+4+7+10+13=35
.....
this is an AP series with d=3
sum of A.P series =(n/2){2a+(n-1)d)
putting d=3 and a=1, we get (n/2)(3n-1) which is the required ans.

ONLY f(n)=(3n-1)n/2 satisfy the two requirements like f(1)=1 and f(n+1)-f(n)=4

The solution is how we can examine that answer by match into the right answer

by putting simple values

we get d as answer

for, f(n+1)-f(n)=(n+1)(n+2)-n(n+1)/2=n+1 for n>1,which contradicts,where f(n)=n(n+1)/2 for f(n)=(3n-1)n/2, f(n+1)-f(n)=3n+1,hence the result

By putting the values 1,2,3... if gives the result of the sequence means that formula is correct. as f(n)=(3n-1)(n)/2

just see the pattern is 1,5 , 12 , 22 , 35 , 51 ... => 4, 7 , 10 , 13 , 16 , 19 ... incise 3 in every time.. then we make a equation like (3n^2-1) / 2

If we know f(3)=12, you just try the options. But that's not beautifil, I admit.