Pentagonal Numbers - What Comes Next?
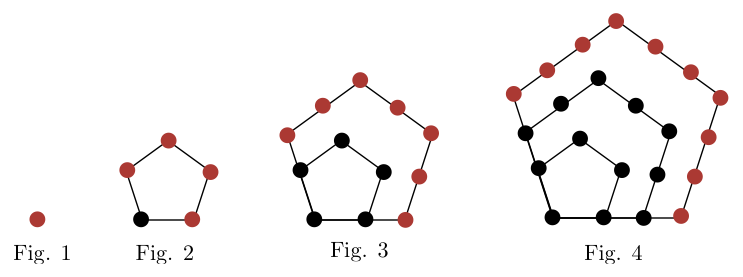What is the number of dots in the next pentagonal figure (i.e. figure 5)?
This question is part of Calvin's set What Makes A Number Pentagonal?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
@Asher Joy I also soled it in the same way :)
1+4+7+10+13=35
@Asher Joy is correct. I also solved it in same way.
Using the law 2 3 n 2 − n ⇒ 2 3 ⋅ 5 2 − 5 = 3 5
The law came from :
a 1 = 1 + 0
a 2 = 2 + 3
a 3 = 3 + 9
a 4 = 4 + 1 8
. . .
0 , 3 , 9 , 1 8 , . . . its the sum of the first n terms of the sequence L n = 3 n − 3 ⇒ S n = 2 n ( 0 + 3 n − 3 ) = 2 3 n 2 − 3 n
Hence: a n = n + S n = n + 2 3 n 2 − 3 n = 2 3 n 2 − n
Log in to reply
There wasn't need for this complication. Simple problem so there are simple methods.
Why S n = 2 n ( 0 + 3 n − 3 ) ?
Log in to reply
L 1 = 3 ( 1 ) − 3 = 0 , L n = 3 n − 3 and there are n terms. & as you know S n = n ⋅ 2 L 1 + L n
35.....no of dots follows series 1 5 12 22 ? ...so next num will be 35 as dif between consecutive num follows sequence 4(5-1) 7(12-5) 10(22-12) ?(x-22).....3 increases in the following sequence so next will be 10+3=13...so x=22+13=35
Log in to reply
you're absolutely correct. this is the simple method that I used also. There is no need to over-complicate things with 'a law'.
First it grows 4 , next 7 , next 10 ... So keeping this logic it will be 22 + 13 = 35
HERE THE PATTERN IS 1 , 5 , 12 , 22 .... OR 4 , 7 , 10 , 13 (DIFFERENCE EVERY TIME) WE CAN WRITE A EQUATION (3n + 1 ),
this is really good website which every engineering student should practice maths with this questions.
it seems the solution is harder to think than the answer.. It's amazing.. thanks btw..
the number of dots in the outermost pentagon in each figure is in A.P. with a=1 and d=3 hence for 5th, dots=5[2(1)+4(3)]/2=35
First it grows 4, next 7 , next 10 ... so , keeping this logic it will grows 13 , 22 + 13 = 35
Each "layer" of the pentagonal has 3 more dots than the previous layer. If the first layer has 1 dot, the second layer has 4 dots, the third layer has 7 dots, and the fourth layer has 10 dots, so the fifth layer has 13 dots. Therefore, for the fifth figure (which will have five layers), the figure will have 1, 4, 7, 10, and 13 in the first, second, third, fourth, and fifth layers, respectively. 1 + 4 + 7+ 10 + 13 = 35.
Each "layer" of the figure has 3 more dots than the previous layer. For the fourth figure, the first layer has 1 dot, the second layer has 4 dots, the third layer has 7 dots, and the fourth layer has 10 dots. Therefore, for the fifth figure (which will have five layers), the figure will have 1, 4, 7, 10, and 13 in the first, second, third, fourth, and fifth layers, respectively. 1 + 4 + 7+ 10 + 13 = 35.