Percentage of cube nearer to its center. (Resubmitted. Previous error was in check.)

Calculus Level 5

What percentage of a cube is nearer to its center than to its surface? The title restated.

I apologize. If you had submitted a correct answer before, then that answer is correct. I did a separate check calculation and I had an error in the check. Since I thought the answer was wrong, I deleted the problem. This is a resubmission.

My computations were done in an unit cube. But, since I am asking for a percentage of volume, you may use any size cube that you find convenient.

I am providing some pictures to assist visualizing the problem. When I first solved this problem, all I had was a verbal description. I learned that using symmetry was my friend. I found a small piece of the entire shape that was amenable to straight forward integration. Finding that piece was the hard part of the problem.

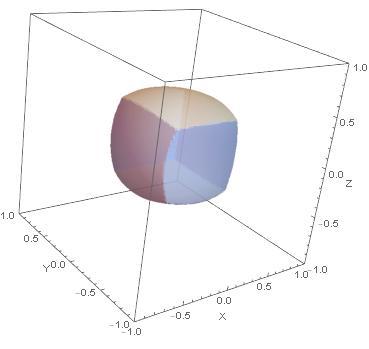
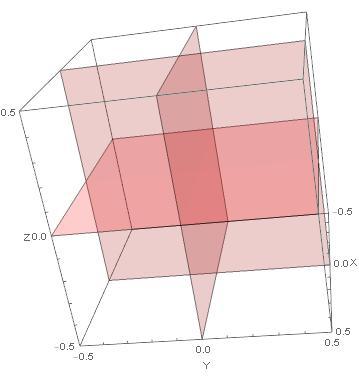
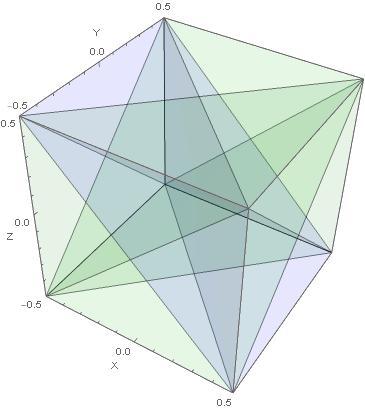
Some checks: a cube of one-half of the edge length of the outer cube has 12.5% of the outer cube's volume. A ball with a radius of one quarter of the outer cube's edge length has π 48 ≈ 6.5 % \frac{\pi}{48} \approx 6.5\% of the outer cube's volume. The average of those estimates, ≈ 9.5 % \approx 9.5\% is a good approximation of the answer; but, it is not the correct answer. I entered the correct answer to 4 places to the right of the decimal point.


The answer is 8.6841.

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

4 solutions

Otto Bretscher
Jan 22, 2019

I consider the cube [ − 1 , 1 ] 3 [-1,1]^3 and focus on the region W W where z ≥ y ≥ x ≥ 0 z\geq y \geq x\geq 0 , with volume 1 6 \frac{1}{6} . We seek the volume of the subregion S S of W W given by x 2 + y 2 + z 2 ≤ 1 − z \sqrt{x^2+y^2+z^2}\leq 1-z , or y ≤ z ≤ 1 − x 2 − y 2 2 y\leq z\leq \frac{1-x^2-y^2}{2} . Such z z exist when y ≤ 1 − x 2 − y 2 2 y\leq \frac{1-x^2-y^2}{2} or x 2 + ( y + 1 ) 2 ≤ 2 x^2+(y+1)^2\leq 2 or y ≤ 2 − x 2 − 1 y\leq \sqrt{2-x^2}-1 . Thus the volume of S S is ∫ 0 ( 3 − 1 ) / 2 ∫ x 2 − x 2 − 1 ∫ y ( 1 − x 2 − y 2 ) / 2 d z d y d x = 1 48 ( 10 − 9 3 + 2 π ) ≈ 0.08684 6 \int_0^{(\sqrt3 -1)/2}\int_{x}^{\sqrt{2-x^2}-1}\int_{y}^{(1-x^2-y^2)/2}dz\ dy\ dx=\frac{1}{48}(10-9\sqrt{3}+2\pi)\approx \frac{0.08684}{6} .

The required percentage is about 8.684 \boxed{8.684} .

0 Helpful 0 Interesting 2 Brilliant 0 Confused
Mark Hennings
Jan 20, 2019

Suppose that the cube has side 2 2 . The desired volume is six times the volume of the intersection of the paraboloid r = 1 1 + cos ⁡ θ r = \tfrac{1}{1+ \cos\theta} (where the spherical polar coordinates are measured with the centre of the cube as origin and the polar axis vertically downwards) with the square pyramid formed by the base of the cube and its centre, and so the volume is equal to 48 48 times the volume of the intersection of the paraboloid with the tetrahedron marked on the diagram.

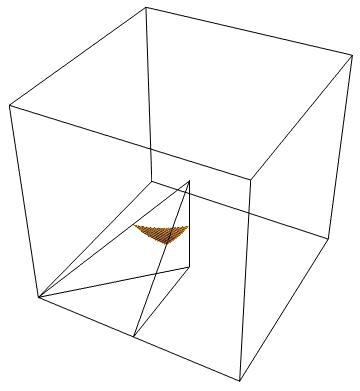
This volume is defined in spherical polar coordinates by 0 ≤ r ≤ 1 1 + cos ⁡ θ 0 \le r \le \tfrac{1}{1 + \cos\theta} , 0 ≤ θ ≤ tan ⁡ − 1 2 0 \le \theta \le \tan^{-1}\sqrt{2} , ϕ ≤ 1 4 π \phi \le \tfrac14\pi and ϕ ≥ { 0 0 ≤ θ ≤ 1 4 π cos ⁡ − 1 ( cot ⁡ θ ) 1 4 π ≤ θ ≤ tan ⁡ − 1 2 \phi \ge \left\{ \begin{array}{lll} 0 & \hspace{1cm} & 0 \le \theta \le \tfrac14\pi \\ \cos^{-1}\big(\cot\theta\big) & & \tfrac14\pi \le \theta \le \tan^{-1}\sqrt{2}\end{array}\right.

Thus the volume is V = 48 ∫ 0 1 4 π d θ ∫ 0 ( 1 + cos ⁡ θ ) − 1 d r ∫ 0 1 4 π d ϕ r 2 sin ⁡ θ + 48 ∫ 1 4 π tan ⁡ − 1 2 d θ ∫ 0 ( 1 + cos ⁡ θ ) − 1 d r ∫ cos ⁡ − 1 ( cot ⁡ θ ) 1 4 π d ϕ r 2 sin ⁡ θ = 4 π ∫ 0 tan ⁡ − 1 2 sin ⁡ θ d θ ( 1 + cos ⁡ θ ) 3 − 16 ∫ 1 4 π tan ⁡ − 1 2 cos ⁡ − 1 ( cot ⁡ θ ) sin ⁡ θ d θ ( 1 + cos ⁡ θ ) 3 = 1 2 π ( 11 − 6 3 ) − 16 [ cos ⁡ − 1 ( cot ⁡ θ ) 2 ( 1 + cos ⁡ θ ) 2 ] 1 4 π tan ⁡ − 1 2 + 8 ∫ 1 4 π tan ⁡ − 1 2 d θ sin ⁡ θ ( 1 + cos ⁡ θ ) 2 sin ⁡ 2 θ − cos ⁡ 2 θ = 8 ∫ 1 3 1 2 d u ( 1 − u 2 ) ( 1 + u ) 2 1 − 2 u 2 − 1 2 π = 16 2 ∫ sin ⁡ − 1 2 3 1 2 π d t ( 2 − sin ⁡ t ) ( 2 + sin ⁡ t ) 3 − 1 2 π \begin{aligned} V & = \; 48 \int_0^{\frac14\pi}\,d\theta \int_0^{(1+\cos\theta)^{-1}}\,dr \int_0^{\frac14\pi}\,d\phi\,r^2\sin\theta + 48 \int_{\frac14\pi}^{\tan^{-1}\sqrt{2}}\,d\theta \int_0^{(1+\cos\theta)^{-1}}\,dr \int_{\cos^{-1}(\cot\theta)}^{\frac14\pi}\,d\phi\,r^2\sin\theta \\ & = \; 4\pi \int_0^{\tan^{-1}\sqrt{2}} \frac{\sin\theta\,d\theta}{(1 + \cos\theta)^3} - 16\int_{\frac14\pi}^{\tan^{-1}\sqrt{2}} \frac{\cos^{-1}(\cot\theta)\sin\theta\,d\theta}{(1 + \cos\theta)^3} \\ & = \; \tfrac12\pi(11 - 6\sqrt{3}) - 16\left[\frac{\cos^{-1}(\cot\theta)}{2(1 + \cos\theta)^2}\right]_{\frac14\pi}^{\tan^{-1}\sqrt{2}} + 8\int_{\frac14\pi}^{\tan^{-1}\sqrt{2}}\frac{d\theta}{\sin\theta(1+\cos\theta)^2\sqrt{\sin^2\theta - \cos^2\theta}} \\ & = \; 8\int_{\frac{1}{\sqrt{3}}}^{\frac{1}{\sqrt{2}}} \frac{du}{(1-u^2)(1+u)^2\sqrt{1-2u^2}} - \tfrac12\pi \; = \; 16\sqrt{2}\int_{\sin^{-1}\sqrt{\frac23}}^{\frac12\pi} \frac{dt}{(\sqrt{2}-\sin t)(\sqrt{2}+\sin t)^3} - \tfrac12\pi \end{aligned} by first performing the integrals with respect to r r and ϕ \phi , integrating by parts and performing the substitutions u = cos ⁡ θ u = \cos\theta and 2 u = sin ⁡ t \sqrt{2}u = \sin t . This last integral can be evaluated via a v = tan ⁡ 1 2 t v = \tan\tfrac12t substitution, and we obtain V = 10 − 9 3 + 2 π V \; = \; 10 - 9 \sqrt{3} + 2 \pi making the required percentage 100 × V 8 = 8.684100488 100 \times \tfrac{V}{8} = \boxed{8.684100488} , which disagrees with the official answer, but coincides with Randolph's proof.

0 Helpful 1 Interesting 2 Brilliant 0 Confused

The offical answer, which I am trying to get changed, came from a high order Monte Carlo evaluation.

A Former Brilliant Member - 2 years, 3 months ago
Frank Petiprin
Feb 23, 2019 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
 
#Using Python
import math
import random
#
#Number of Trials using Random numbers
#
Trials=20000000
ccenters,cedges=0,0
SurfaceD=[0]*6
for j in range(1,Trials+1):
    x,y,z=random.uniform(0,1),random.uniform(0,1),random.uniform(0,1)
    dcnt=math.sqrt((x-.5)**2+(y-.5)**2+(z-.5)**2)
    SurfaceD[0],SurfaceD[1],SurfaceD[2],SurfaceD[3]=x,1-x,y,1-y
    SurfaceD[4],SurfaceD[5]=z,1-z
    SurfaceD.sort()
    smplane=SurfaceD[0]
    if(smplane<dcnt):
        cedges+=1
    else:
        ccenters+=1
print(Trials,ccenters,cedges,(ccenters/Trials)*100,'%',(cedges/Trials)*100,'%')

#Four Runs At 20000000 Trials each.
20000000 1733515 18266485 8.667575 % 91.332425 %

20000000 1737104 18262896 8.685519999999999 % 91.31448 %

20000000 1737309 18262691 8.686544999999999 % 91.313455 %

20000000 1735069 18264931 8.675345 % 91.32465499999999 %

20000000 1738403 18261597 8.692015 % 91.307985 %

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Good job at your Monte Carlo evaluations. The present official answer came from a high order Monte Carlo. That is why it is subtly wrong. I am trying to get offical answer changed to the closed form solution.

A Former Brilliant Member - 2 years, 3 months ago

I used a cube radius, one half of the edge length) of 1 2 \frac12 .

The expression describing the shape: ( radius + x ) 2 > x 2 + y 2 + z 2 ∧ ( x − radius ) 2 > x 2 + y 2 + z 2 ∧ ( radius + y ) 2 > x 2 + y 2 + z 2 ∧ ( y − radius ) 2 > x 2 + y 2 + z 2 ∧ ( radius + z ) 2 > x 2 + y 2 + z 2 ∧ ( z − radius ) 2 > x 2 + y 2 + z 2 (\text{radius}+x)^2>x^2+y^2+z^2\land (x-\text{radius})^2>x^2+y^2+z^2\land (\text{radius}+y)^2>x^2+y^2+z^2\land \\ (y-\text{radius})^2>x^2+y^2+z^2\land (\text{radius}+z)^2>x^2+y^2+z^2\land (z-\text{radius})^2>x^2+y^2+z^2

I supplied a picture of the shape in the problem definition.

I integrated over a piece that was 1 48 th \frac1{48}^{\text{th}} of the total volume of the shape:

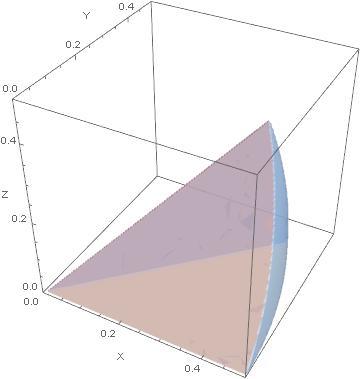
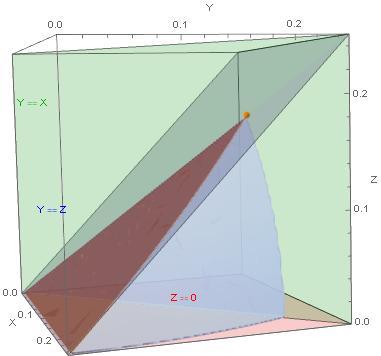
In the cube, there are six faces. In each face, there are four quadrants. In each quadrant, there are two mirrored sectors. Six times four times two is forty eight sectors altogether. The orange point, at an extremity of the piece is at { 3 − 1 4 , 3 − 1 4 , 3 − 1 4 } \{\frac{\sqrt{3}-1}{4},\frac{\sqrt{3}-1}{4},\frac{\sqrt{3}-1}{4}\} .

The volume of that piece of the unit cube is 1 384 ( − 9 3 + 2 π + 10 ) ≈ 0.00180918760172 \frac{1}{384} \left(-9 \sqrt{3}+2 \pi +10\right) \approx 0.00180918760172 .

The complete integral, with the correction for the size of cube used (I used an unit cube so that term was 1): 48 ( 2 radius ) 2 ( ∫ 0 1 4 ( 3 − 1 ) ∫ 0 y ∫ y 1 4 ( − 4 y 2 − 4 z 2 + 1 ) 1 d x d z d y + ∫ 1 4 ( 3 − 1 ) 1 2 ( 2 − 1 ) ∫ 0 1 2 − 4 y 2 − 4 y + 1 ∫ y 1 4 ( − 4 y 2 − 4 z 2 + 1 ) 1 d x d z d y ) ⟹ ( 2 radius ) 2 ( 48 192 ( 9 − 5 3 ) + 48 384 ( 3 + 2 π − 8 ) ) = = ( 2 radius ) 2 48 384 ( − 9 3 + 2 π + 10 ) = = ( 2 radius ) 2 1 8 ( − 9 3 + 2 π + 10 ) ≈ ( 2 radius ) 2 0.0868410048824613543972837116258 48\ (2\ \text{radius})^2 (\\ \int _0^{\frac{1}{4} \left(\sqrt{3}-1\right)}\int _0^y\int _y^{\frac{1}{4} \left(-4 y^2-4 z^2+1\right)}1\,dx\,dz\,dy+ \int _{\frac{1}{4} \left(\sqrt{3}-1\right)}^{\frac{1}{2} \left(\sqrt{2}-1\right)}\int _0^{\frac{1}{2} \sqrt{-4 y^2-4 y+1}}\int _y^{\frac{1}{4} \left(-4 y^2-4 z^2+1\right)}1\,dx\ dz\,dy) \Longrightarrow \\ (2\ \text{radius})^2\left(\frac{48}{192} \left(9-5 \sqrt{3}\right) + \frac{48}{384} \left(\sqrt{3}+2 \pi -8\right)\right) == \\ (2\ \text{radius})^2\frac{48}{384} \left(-9 \sqrt{3}+2 \pi +10\right) == \\ (2\ \text{radius})^2 \frac{1}{8} \left(-9 \sqrt{3}+2 \pi +10\right) \approx \\ (2\ \text{radius})^2 0.0868410048824613543972837116258 .

Some of the intermediate indefinite integrals: ∫ 1 d x ⟹ x ∫ ( 1 4 ( − 4 y 2 − 4 z 2 + 1 ) − y ) d z ⟹ − y 2 z − y z − z 3 3 + z 4 ∫ ( − y 2 z − y z − z 3 3 + z 4 ) d z ⟹ − y 2 z 2 2 − y z 2 2 − z 4 12 + z 2 8 \int 1 \, dx \Longrightarrow x\\ \int \left(\frac{1}{4} \left(-4 y^2-4 z^2+1\right)-y\right) \, dz \Longrightarrow -y^2 z-y z-\frac{z^3}{3}+\frac{z}{4}\\ \int \left(-y^2 z-y z-\frac{z^3}{3}+\frac{z}{4}\right) \, dz \Longrightarrow -\frac{y^2 z^2}{2}-\frac{y z^2}{2}-\frac{z^4}{12}+\frac{z^2}{8}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

1 pending report

Vote up reports you agree with

×

Problem Loading...

Note Loading...

Set Loading...