Percentage of the total area?
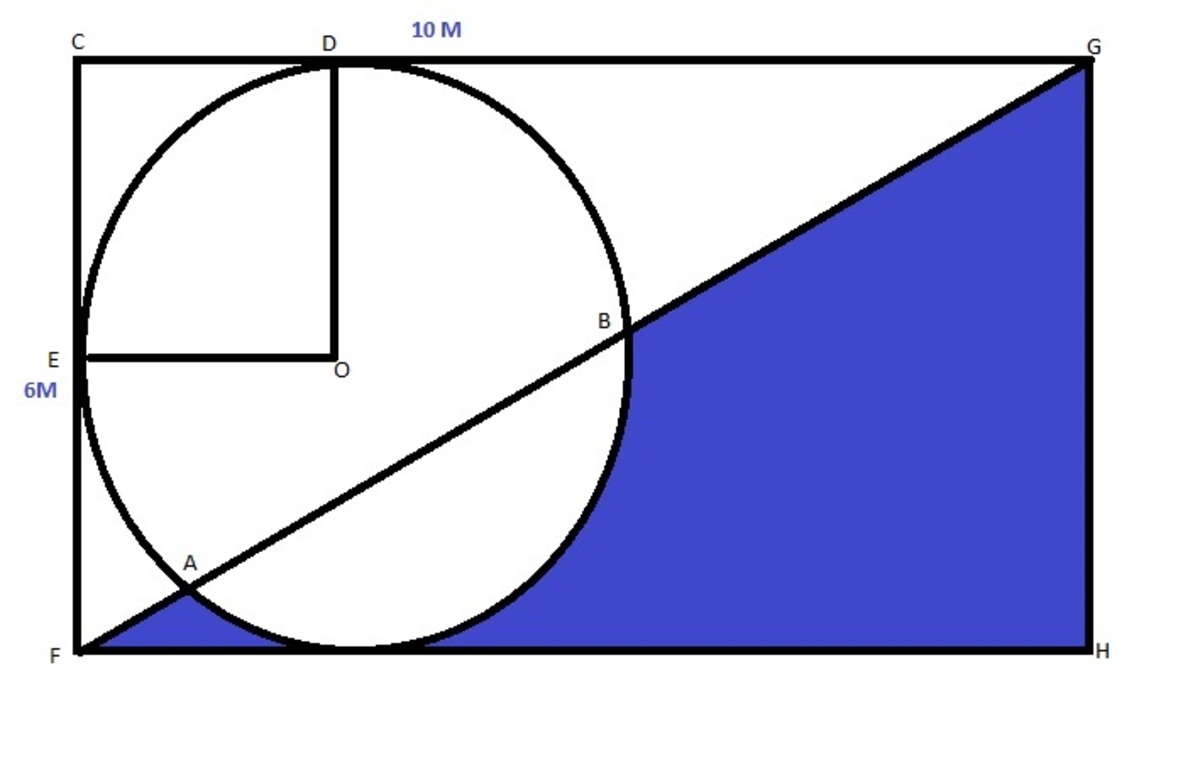
What percent of the total area of the rectangle is the blue colored region ?. The radius of the circle OE, OD is 3 meters. FCGH is a rectangle with FC = 6meters and CG = 10meters.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the co-ordinates of F be (0,0). The co-ordinates of O are (3,3).
The equation of the circle with center at (3,3) and radius 3 can be written as
(x-3)^2 + (y-3)^2 = 9 --------------------------------(1)
Equation of the diagonal FG can be written as y = 0.6*x---------------------------(2)
Substituting (2) in (1) and solving for x will yield the x coordinates of points A and B. Y coordinates of A and B can be found using equation (2).
Substituting (2) in (1) yields
1.36 x^2 -9.6 x + 9 = 0
Solving the quadratic equation yields two values of X ( x1 , x2) which are equal to x1= 5.9458 and x2 = 1.113
The co-ordinates A and B can be determined as y = 0.6*x and so the co-ordinates of A are (1.113, 0.6678) and B are (5.9458,3.56748)
The length of AB can be calculated as =sqrt((x2-x1)^2+(y2-y1)^2) =sqrt((5.9458-1.113)^2+(3.56748-0.6678)^2) =sqrt(23.355955840000007+8.4081441024) =sqrt(31.76409994240001) =5.635964863481674=5.636
The area of the triangle AOB can be calculated using Heron's formula The area is given by: Area = sqrt( p* ( p−a ) (p−b) ( p−c) )
where p is half the perimeter, or
p = (a + b + c )/2
Sides: a = 3 b = 3 c = 5.636
Area of Triangle AOB = 2.9 -------------------------(3) Perimeter: p = 11.636 Semiperimeter: s = 5.818
Angle ∠ ABO = α = 20.06° = 20°3'36″ = 0.35 rad Angle ∠ BAO = β = 20.06° = 20°3'36″ = 0.35 rad Angle ∠AOB = γ = 139.88° = 139°52'47″ = 2.441 rad
Area of the sector AOB which subtends 139°52'47″ in the center is pi* 9 * 139.88/360 = 10.986 sqm.
Area of the circle below the chord AB = Area of Sector AOB - Area of Triangle AOB = 10.986 - 2.9 = 8.086 sqm.
Hence area of the blue colored region = Area of Triangle FGH - Area of the circle below the chord AB = 30 - 8.086 = 21.914
So percent of the blue colored area = (21.914/60) * 100 = 36.52 percent